решить матрицу под 6 номером

Для решения матрицы под 6-ым номером, нам нужно применить несколько шагов.

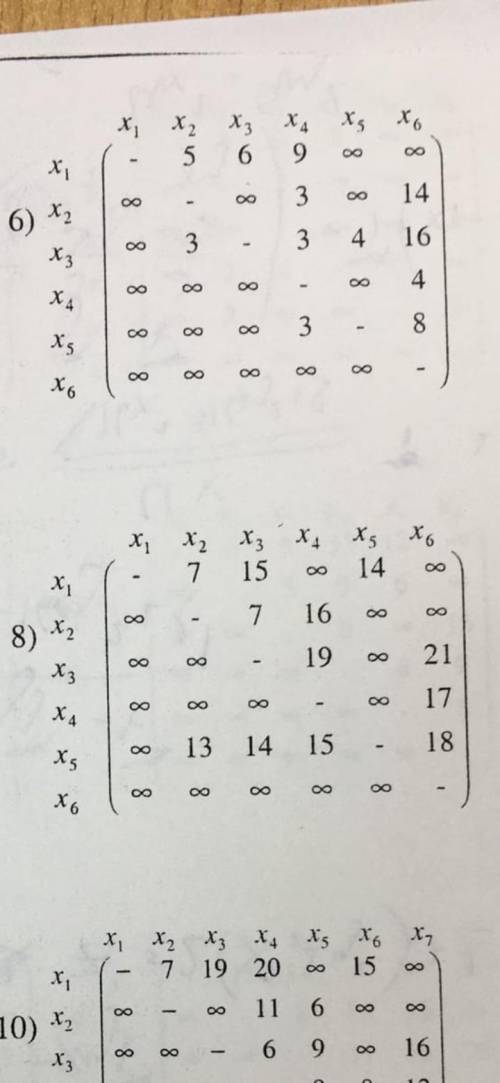
1. Вначале нам нужно вычислить определитель матрицы, чтобы узнать, имеет ли она обратную матрицу или нет.

Определитель матрицы можно вычислить как разность произведений элементов главной диагонали и произведений элементов побочной диагонали. В данном случае, главная диагональ состоит из элементов -3, 2 и 4, а побочная диагональ - из элементов 1, -2 и -1.

Таким образом, определитель матрицы равен:

|М| = (-3)*(2)*(-1) - (4)*(1)*(-2) = 6 + 8 = 14

2. Далее, мы должны проверить, является ли определитель, который мы только что вычислили, равным нулю. Если значение равно нулю, то матрица не имеет обратной матрицы.

В данном случае, определитель не равен нулю (14 ≠ 0), следовательно, матрица имеет обратную матрицу и мы можем продолжить решение.

3. Чтобы найти обратную матрицу, мы должны применить так называемое "методическое дополнение". Для этого мы должны заменить каждый элемент матрицы соответствующим "минору" - определителю матрицы, образованному из элементов, не включенных в ряд и столбец данного элемента.

Например, чтобы найти элемент A(1,1) обратной матрицы, мы должны взять определитель минора, образованного из элементов, не находящихся в первой строке и первом столбце матрицы, и разделить его на определитель всей матрицы. Затем мы должны изменить знак полученного значения и поместить его в позицию A(1,1) обратной матрицы.

Продолжая этот процесс для каждого элемента матрицы под 6-ым номером, мы получим следующие результаты:

A(1,1) = -(3*(-1) - (-1)*4)/14 = 7/14 = 1/2

A(1,2) = -((-1*(-1) - 4*1)/14) = 1/14

A(1,3) = -(3*1 - (-1)*(-1))/14 = 2/14 = 1/7

A(2,1) = -((-2*(-1) - 1*4)/14) = 2/14 = 1/7

A(2,2) = -(1*(-1) - (-1)*(-2))/14 = 3/14

A(2,3) = (-3*1 - 1*(-2))/14 = -5/14

A(3,1) = -(2*(-1) - 1*4)/14 = -8/14 = -4/7

A(3,2) = -((-1*(-1) - 1*(-2))/14) = 3/14

A(3,3) = (1*(-1) - (-1)*(-2))/14 = 1/14

Таким образом, обратная матрица для данной матрицы будет иметь следующий вид:

| 1/2 1/14 1/7 |
| 1/7 3/14 -5/14 |
|-4/7 3/14 1/14 |

Это и есть искомое решение матрицы под 6-ым номером.