Решить иррациональное неравенство. 
как можно подробнее
ответ ( ; +∞)
; +∞)
Другие вопросы по теме Математика
Популярные вопросы
- Уявлення про нові пригоди томас сойера...
3 - График линейной функции y=kx+b параллелен графику функции y=12x-1 и...
3 - Складить невелике повидомленя (5-8 предложений) про рослыни сымволи...
1 - Выберите слово, которое при изменении частеречной принадлежности не...
1 - Чему равно q(q 1),если в прогрессии b1+b4=35,b2+b3=30?...
1 - Через вершину к равнобедренного треугольника akd проведена прямая ef...
1 - По каноническому уравнению кривой второго порядка определить тип кривой....
1 - Над словами с окошками укажи часть речи, выделяй части слова с окошками...
1 - Определите, сколько раз звуки, составляющие слово лён, встречаются в...
1 - 1) назрин играла в компьютерную игру. при этом она попала в цель 3 раза...
3
ОДЗ:
Решение: возведём обе части неравенства в квадрат:
Первый корень не подходит по ОДЗ. Значит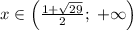 .
.