Математика: решить интеграл: 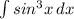. ответ должен быть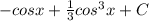

решить интеграл: $\int\limits {sin^3x} \, dx$ . ответ должен быть $- cosx+\frac{1}{3} cos^3x+ C$

Ответы

Aelly 26.07.2021 20:49

Пошаговое объяснение:

∫sin³xdx=∫sin²xsinxdx=

по формуле sin²x=1-cos²x

=∫(1-cos²x)sinxdx=

внесем cosx под знак дифференциала

=-∫(1-cos²x)d(cosx)=

заменим переменную cosx=y

=-∫(1-y²)dy=-∫dy+∫y²dy=-y+y³/3+c

заменим y=cosx

=-cosx+(1/3)cos³x+c

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Математика

murzyatyan 03.09.2020 15:22

Десятковый дроб в обычное число...

пллсыео 03.09.2020 15:22

10-5•(на одну целую пять десятых)-(одна третяя)=...

molnij63 03.09.2020 15:22

обчисли: (2.8:0.01+28.77:0.1):8...

fjjjfg 03.09.2020 15:22

Сколько чисел в натуральном ряду между 34 и 100?...

ДианаDi1111 03.09.2020 15:22

Лиана1574 03.09.2020 15:23

Скільки цілих розв язків має нерівність...

nastiasteinoxz34d 03.09.2020 15:23

samaya2009 03.09.2020 15:23

ddiana004 03.09.2020 15:23

sququ1 03.09.2020 15:23