решить Хотя бы какую-то часть


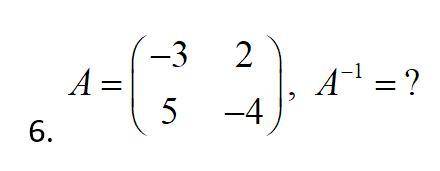


Другие вопросы по теме Математика
Популярные вопросы
- Биссектрисы углов a и b треугольника abc пересекаются в точке...
1 - Listen! and he sang the song. dorothy didn t like it. she said...
3 - Вторые формы слов take fall see say. give fly sit...
1 - Сторона правильного треугольника равна 37 корень из трех. найдите...
2 - Yes, i will, said the scarecrow. what will you give to ozma? i...
1 - 1) из одной точки проведены две касательные к окружности. докажите,...
2 - 1. преобразуйте в многочлен. а. 2c *(1+-2)*(c+1) б.(y+2)^2 -2y*(y+2)...
1 - Заранее . present indefinite or the future indefinite. 1. if he...
1 - Написать реферат на тему космонавты...
3 - Translate the sentences from russian into english using model...
2
Пошаговое объяснение:
1)
2)
3)
для вычисления обратной матрицы запишем матрицу А, дописав к ней справа единичную матрицу:
теперь чтобы найти обратную матрицу, преобразуем левую часть полученной матрицы в единичную.
1-ую строку делим на -3
1 строку * 5 к 2ой добавляем 1 строку
2-ую строку делим на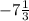
и последнее 2ую * (2/3) и к 1 строке добавляем 2ую
и вот
4)
определитель матрицы А:
∆A = 1*1 - 2*1 = -1
nак как A невырожденная матрица, то существует обратная матрица A⁻¹
Умножим справа обе части уравнения на A⁻¹: X·A·A⁻¹ = B·A-1, откуда находим, что X = B·A⁻¹
найдем обратную матрицу A⁻¹.
транспонированная матрица
aлгебраические дополнения
A₁₁ = (-1)¹⁺¹ *1 = 1; A₁₂ = (-1)¹⁺² *1 = -1;
A₂₁ = (-1)²⁺¹ *2 = -2; A₂₂ = (-1)²⁺² *1 = 1;
обратная матрица
тогда