решить (х-2) в степени: (х^2-6х+8)>1
Или же
(х-2)^((х^2)-6х+8)>1
На фото это номер 4
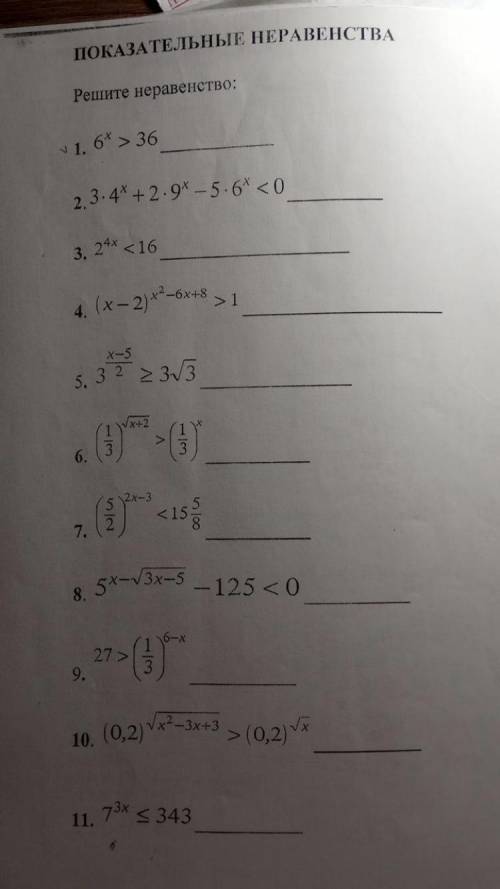
Другие вопросы по теме Математика
Популярные вопросы
- Вычисли значения вырождения используя правило деления суммы на число (30+12)÷3...
2 - Запиши название книги о защитниках отечества которые ты читал...
2 - Каких героев защищавших нашу родину ты знаешь?...
2 - Придумайте тему для детектива. хочу попробовать написать свой первый детектив,...
1 - Поле в какой природной зоне находиться?...
3 - Придумать предложение на слово пассажир...
2 - Раздели делимое и делитель на 5 как это делать? 400: 5...
3 - Выполнить действия. ответ выразил в возможно более крупных единицах измерения....
2 - Выполнить действия. ответ выразил более крупных единицах измерения 5ц6кг+28кг...
1 - Вмоскве стоят два папятника и минину ,напиши можно ли сказать что это памятник...
1
Сначала рассмотрим первый случай:
(x-2)^(x^2-6x+8) > 1
Заметим, что число 1 в данном случае является положительным, поэтому нам необходимо рассмотреть два варианта:
1) Если (x-2) > 1, то неравенство будет выполняться для любого положительного показателя степени.
2) Если (x-2) < 1, то неравенство будет выполняться только для четных положительных показателей степени, так как в этом случае отрицательное число будет возведено в некую четную степень и станет положительным.
Рассмотрим второй случай:
(x-2)^((x^2)-6x+8) > 1
В данном случае показатель степени представлен функцией x^2-6x+8. Чтобы понять, в каких интервалах данное неравенство будет выполняться, необходимо проанализировать знак функции.
Заметим, что факторизация функции x^2-6x+8 дает нам (x-2)(x-4).
Теперь рассмотрим интервалы числовой оси, где x^2-6x+8 является положительным и отрицательным:
1) Если x < 2, то оба множителя (x-2) и (x-4) в данном примере будут отрицательными, так как они меньше 0. Таким образом, (x-2)^(x^2-6x+8) будет положительным, и неравенство не выполняется.
2) Если x > 4, то оба множителя (x-2) и (x-4) в данном примере будут положительными, так как они больше 0. Таким образом, (x-2)^(x^2-6x+8) будет положительным, и неравенство выполняется.
3) Если 2 < x < 4, то множитель (x-2) будет положительным, а (x-4) будет отрицательным. В этом интервале (x-2)^(x^2-6x+8) будет отрицательным и неравенство не выполняется.
Таким образом, неравенство выполняется только при x > 4, а также в любом интервале (x-2) > 1.