Математика: решить. Геометрия 7 класс(в 28 найти угол В)

решить. Геометрия 7 класс
(в 28 найти угол В)

Ответы

PsyhovanayaPechenka 11.10.2020 12:37

B = 30’
Якшо прямий є 90 а даний кут 30 то третій =60
Оскільки це бісектриса і ділить кут навпіл то B=30

ПОКАЗАТЬ ОТВЕТЫ

nataliamakarov3 11.10.2020 12:37

Задача №28

Как мы видим угол В делится пополам биссектрисой BD. Треугольник САВ - прямоугольный. Сумма всех внутренних углов в треугольнике = 180°.

Угол В = 180° - 30° - 90° = 60°

Задача №29

Для начала вычислим угол А.

Угол А = 180° - 30° - 90° = 60°

Угол САD равен углу DAB, так как AD - биссектриса.

Угол DAB = 30°

Угол ADB = 180° - 30° - 30° = 120°

Как мы знаем, катет, лежащий напротив угла в 30° равен половине гипотенузы. Применим теорему Пифагора, обозначив за сторону АС:

$x^2 + 900 = 4x^2\\\\x^2 - 4x^2 = -900\\\\-3x^2 = -900\\\\x^2 = 300\\\\x= 10\sqrt{3}$

Как мы знаем, катет, лежащий напротив угла в 60° больше второго катета в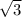 $\sqrt{3}$ раз. Применим теорему Пифагора, обозначив за отрзок СD:

$300 + x^2 = 4x^2\\\\ 300 = 3x^2\\\\x^2 = 100\\\\ x = 10\\\\$

CD = 10 см. И этот катет лежит напротив угла в 30°. Следовательно искомая гипотенуза-биссектриса AD равна 20 см.

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Математика

лерунька7 30.08.2019 18:10

nastylamyr2999 30.08.2019 18:10

Реши уравнение : у : 4,2=3.4 : 5.1...

vikinagirich 30.08.2019 18:10

tatuxa223 30.08.2019 18:10

викуля1101 30.08.2019 18:10

karinasurshkose 30.08.2019 18:10

Найди значений выражение 19: (22875: 75+3561)=...

hola174 30.08.2019 18:10

Alidisa1202 30.08.2019 18:10

mit210404 30.08.2019 18:10

ПрохладныйВетер 30.08.2019 18:10