1. Математика
  2. Решить два примера. Photomath

Решить два примера. Photomath не


Решить два примера. Photomath не
Решить два примера. Photomath не

КУМИР566 КУМИР566    1   27.01.2022 10:20    0

Ответы
kristail2003101979 kristail2003101979  27.01.2022 10:30

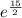
1. e^{\frac{15}{2}}

2. x = 0

Пошаговое объяснение:

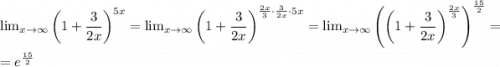
1. \lim_{x \to \infty} \left(1+\dfrac{3}{2x}\right)^{5x}= \lim_{x \to \infty} \left(1+\dfrac{3}{2x}\right)^{\frac{2x}{3}\cdot\frac{3}{2x}\cdot5x}= \lim_{x \to \infty} \left(\left(1+\dfrac{3}{2x}\right)^{\frac{2x}{3}}\right)^{\frac{15}{2}}=\\
=e^{\frac{15}{2}}

2. Потенциальные точки разрыва: x = 0 и x = 4. Рассмотрим односторонние пределы в этих точках.

В точке x = 0:

\lim_{x \to 0-0} y= \lim_{x \to 0-0} x=0\\
 \lim_{x \to 0+0}y= \lim_{x \to 0+0} \dfrac{4}{x}=+\infty

Это разрыв второго рода.

В точке x = 4:

\lim_{x \to 4-0} y= \lim_{x \to 4-0} \dfrac{4}{x}=1\\
 \lim_{x \to 4+0} y= \lim_{x \to 4+0}1=1

Поскольку f(4) = 1 и односторонние пределы равны значению функции в этой точке, функция на данном промежутке непрерывна.


Решить два примера. Photomath не
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
Катяhfhfyvdhvxd Катяhfhfyvdhvxd  20.03.2021 21:00
Рост младшего брата равен 1,18 м. Каков приблизительный рост старшего брата? ответ запиши в сантиметрах...
axudatyan axudatyan  20.03.2021 21:00
Найти производную tg(y)=4xy-5x^2...
Danila29012006 Danila29012006  20.03.2021 20:57
Одна сторона прямоугольника на 6 см короче другой.Найдите площадь этого прямоугольника,если его периметр равен 60 см.Сколько квадратов со стороной 6 см имеют вместе такую...
Tetafir Tetafir  20.03.2021 20:57
хелп. ответ только правильной​...
gulbakhar gulbakhar  20.03.2021 20:55
Найти частное решение линейного однородного дифференциального уравнения второго порядка с постояннымикоэффициентами, удовлетворяющее заданным начальнымусловиям.y -2y +5y=0,y(0)=5,y...
котикДжеек котикДжеек  20.03.2021 20:47
У саду площею 70 га ростуть яблуні, сливи і груші. Яблуні займають3/5 площі саду. Сливамизасаджено на 30 га менше, ніж яблунями. На квадратній площі, що залишилася, ростутьгруші....
Phkgd Phkgd  20.03.2021 20:46
Pomyślałem pewna liczbę ,podniosłem ją do kwadratu i dodałem do tego pomyślana liczbę. Otrzymałem wtedy 90. Jaka liczbę pomyślałem.​...
Хэйллис Хэйллис  20.03.2021 20:46
1.Дополните:(8х-)²=...-...+9 2.Упростите выражение:3х+5у-7,5-8,12у= 3.Вычислите:а)-2х(3х-5у)= б)(5х+3)²= в)(4а-7)(4а+7)= г)(2х²)³×14х²=...
arrrtem arrrtem  20.03.2021 20:46
Сделать задания (выш. мат.) ​...
salatinabbasova salatinabbasova  20.03.2021 20:45
у двох сплавах мідь і цинк відносяться як 5:2 і 3:4 відповідно. На скільки кілограмів одного із сплавів треба взяти більше, щоб одержати 28 кг нового сплаву з рівним вмістом...

Популярные вопросы