решить:

Докажите, что выражение 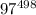-1 делится на 997

Следует, во-первых, показать, что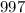 является простым числом. Делается это так: у любого составного числа 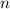есть хотя бы один делитель, отличный от единицы, не превосходящий 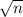. В самом деле, если такого делителя нет, то найдутся два делителя, больших 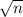, а это невозможно. Поэтому достаточно проверить наличие делителей от 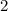до 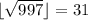. Из них нужно проверять только простые: 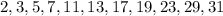, что сделать уже совсем нетрудно.

По малой теореме Ферма мы знаем, что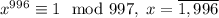 . .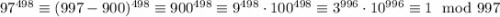