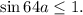Решить докажите что 
Другие вопросы по теме Математика
Популярные вопросы
- Название горы высота которой 7495 метров...
3 - Match the adjectives below to the job descriptions challenging stressful...
3 - ответьте письменно на вопросы. 1) Как беспилотные автомобили определяют...
2 - Дайте назви таким солям: CaSO4, Na2CO3,MnCl2, Fe(NO3)3, Ва(NO3)2....
3 - Перепишите дроби в десятичной форме a)5/10 b)1 21/100 c)3107/10000 d)-...
3 - Каким в музыке И. Стравинского предстаëт фантастический мир Кащеева царства?...
1 - Твір ти знаєш, що ти - людина...
3 - Тест по информатике 9 класс...
3 - с задачей ::На дереве было 5 груш::На другом дереве было 8 яблок..сколько...
3 - 1. Найдите значение выражения 25х+12y при х=2/5, у=1/4 2. Решите уравнение:...
3
Воспользуемся несколько раз формулой
поскольку