решить. Доказать, что если z=ln9x+e^-y), то
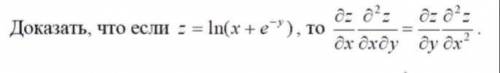
Другие вопросы по теме Математика
Популярные вопросы
- 50 составить схему взаимосвязи органов дыхания с органами кровообращения...
3 - Проверочное слово к слову неподвластный...
3 - Доклад по биологии на тему рак легких...
1 - Найдите площадь сферы, радиус которой равен 6см....
1 - За 2 часа автомобиль проехал 120 км. сколько километров он проехал за 50 минут?...
1 - Записать c^80 в виде степени с показателем 10...
1 - Проявление добра в произведениях примеры и распишите...
2 - Пример: 2(7- а)- 5а=-14+2а-5а почему 14 получается с минусом? ведь 2*7=14...
1 - Из 30 килограмм семян получается 6 кг...
3 - Скажите по казахскому 5 слов которые отвечают на вопросы (кімге неге қайда)...
1
подставляем в равенство: