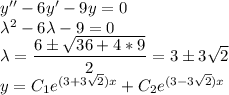решить дифференциальные уравнения:
y''-6'-9y=0
Другие вопросы по теме Математика
Популярные вопросы
- Проходной ЕГЭ по специальностям Восточно-Сибирская государственная...
3 - Проходной ЕГЭ по специальностям Владимирский юридический институт...
3 - Проходной ЕГЭ по специальностям Владимирский государственный...
1 - Проходной ЕГЭ по специальностям Владимирский институт бизнеса...
2 - Проходной ЕГЭ по специальностям Московский государственный университет...
3 - Проходной ЕГЭ по специальностям Ковровская государственная технологическая...
1 - Проходной ЕГЭ по специальностям Волгоградский юридический институт...
3 - Проходной ЕГЭ по специальностям Московский гуманитарно-экономический...
1 - Проходной ЕГЭ по специальностям Волгоградская академия МВД РФ...
2 - Проходной ЕГЭ по специальностям Волгоградский государственный...
2
1)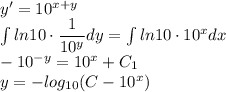
__________________________
2)