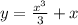Решить дифференциальное уравнение y'=x^2+1 если при x=0; y=0
Другие вопросы по теме Математика
Популярные вопросы
- Задание 2. Запишите условие и решите задачу. В саду 78 деревьев, из...
2 - До ть будь ласка зробіть всі завдання...
2 - По рисунку обьясните свойства планеты земля а) вид движения...
3 - Определите период данной функции: y=12tan(2x+3) Определите период данной...
2 - Составь ответ на вопрос. Аргументируй свой ответ. (4 б) Чем земледелие...
2 - Через какой пролив человек около 35 тыс. лет назад проник в Северную...
2 - В крестьянском хозяйстве Малкални два поля были засеяны пшеницей. Хотя...
1 - Берілген сөздер мен сөйлемге өздік және өзгелік етіс жұрнақтарын жалғап...
3 - Запиши предложения, вставляя пропущенные буквы. Составь схемы предложений...
1 - С какими государствами граничил Кангюй...
1
Пошаговое объяснение:
Ну-с, погнали:
y'=x^2+1
Интегрируем левую и правую часть:
Поскольку y(0)=0, то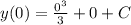 => C=0
=> C=0
Значит ответ: