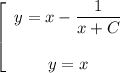Решить дифференциальное уравнение y штрих=(x-y)^2+1 если можно поточнее
Другие вопросы по теме Математика
Популярные вопросы
- Задание 2. Составить небольшой рассказ (5-6 предложений) на тему «Если бы у меня...
2 - -- 34(S1-34. а) Прямоугольник разбили на квадра-ты. Найди площади квадратов, сложиих...
1 - Фермер решил засеять горохом участок земли прямоугольной формы, длина которого...
3 - Е алгебраических выражений на множители с фор 1ого умножения. Урок 3ножители многочлен...
3 - «Пурпурові вітрила» лист до героя ( Ассоль або Грей)...
3 - БОЛЬШЕ НЕТУ Относительная электроотрицательность элементов увеличивается в ряду:...
3 - Обчисліть (0,6)-³ + (1 13 дробь)-² - 7,26...
3 - Как называется занимательный рассказ о необыкновенных часто фантастических событиях...
2 - Үрақтарға жауап бер: 1) Мейрамбек аспандагы бұлттарды нелерге ұқсатты?2) Бұл көктем...
1 - Bilde satze ist ein das hund und klein ist sie schon rot der hahn ist? das huhn...
2
замена y-x=u(x);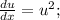
одно из решений u=0; y-x=0; y=x;
ответ: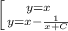
Пусть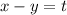 , тогда
, тогда  откуда
откуда 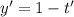 , частное решение y - x=0 откуда у = х, тогда получаем
, частное решение y - x=0 откуда у = х, тогда получаем
Последнее дифференциальное уравнение является уравнением с разделяющимися переменными.
Выполнив обратную замену, получим
Получили общее решение дифференциального уравнения
ответ: