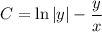решить дифференциальное уравнение y^2dx=(xy-x^2)dy
это однородное диф ур-е. т. е с заменой y=u*x и y'=u'x+u
Другие вопросы по теме Математика
Популярные вопросы
- Раскройте скобки, употребив глаголы в Present Perfect or Past...
1 - Уравнение реакции (молекулярное и ионное): 1.Серная кислота...
2 - 3 - тпасырма. Аудиомәтінді тыңдап, сұрақтарға жауап бер....
2 - Алгебра, делимость. Докажите, что n² + 1 ⋮ 125...
3 - present simple form.1) A cheetah (run) very fast.2) Frogs (live)...
1 - 747 Өрнектердің мәндерін есептемей ақ мәндері тең Өрнектердің...
2 - Задание с функцией ЕСЛИ в Excel...
3 - (сделать след от ботинка с расчетами на двойном листке). 48...
3 - 884. Балаларға сыйлыққа кәмпиттердің бірдей орамдары сатылып...
1 - ЖАЗЫлым 9-тапсырма. Мәтіннен деректі, дерексіз зат есімдерді...
1
решение на фотографии
Пусть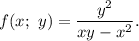 Тогда
Тогда 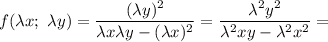
Имеем дифференциальное уравнение, однородное относительно переменных.
Подстановка: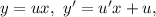 где
где 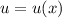
Имеем:
Обратная подстановка:
ответ: