1. Математика
  2. Решить дифференциальное

Решить дифференциальное уравнение (xy y)dx (x-xy)dy=0.и найти его частное решение удовлетворяющее условия при x=1 ,y=1

Лара1512 Лара1512    2   10.07.2019 06:30    0

Ответы
Annet483 Annet483  30.08.2020 15:18
Supondré que es esta: 
 
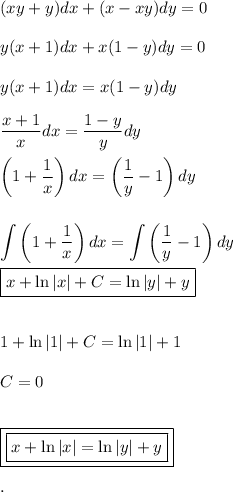
           (xy+y)dx+(x-xy)dy=0\\ \\
y(x+1)dx+x(1-y)dy=0\\ \\
y(x+1)dx=x(1-y)dy\\ \\
\dfrac{x+1}{x}dx=\dfrac{1-y}{y}dy\\ \\
\left(1+\dfrac{1}{x}\right)dx=\left(\dfrac{1}{y}-1\right)dy\\ \\ \\
\displaystyle
\int\left(1+\dfrac{1}{x}\right)dx=\int\left(\dfrac{1}{y}-1\right)dy\\ \\
\boxed{x+\ln|x|+C=\ln|y|+y}\\ \\ \\
1+\ln|1|+C=\ln|1|+1\\ \\
C=0\\ \\ \\
\boxed{\boxed{x+\ln|x|=\ln|y|+y}}
\\ \\.
ПОКАЗАТЬ ОТВЕТЫ
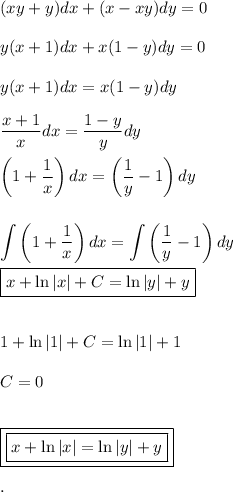
Другие вопросы по теме Математика
Nadachansky Nadachansky  14.07.2019 14:10
За 10 дней кот матроскин заготовил (дробь) две третих необходимого на зиму количества дров . какую часть дров он успевал заготовить за 1 день ? какую часть дров...
nikitoschenko nikitoschenko  14.07.2019 14:10
Вконференции принимали участие 19 уёных. после конференции каждый из них отправил 2 или 4 письма другим учёным, бывшим на конференции. каждый из участников получил...
Bisspector Bisspector  14.07.2019 14:10
Из 20 кг кедрових орехов можно получитьт 5 кг масла. сколко кедрових орехов надо взять чтобы получить 20 кг масла? пишите условия...
Рвововоаоа Рвововоаоа  14.07.2019 14:10
Объяснить устно и решить столбиком примеры 768/8 2367/3 8334/6 9268/7...
ОВОВОВОВо ОВОВОВОВо  14.07.2019 14:10
Реши . вычисли и запиши ответ. миша нарисовал на своем флажке 6 рядов маленьких звёздочек-по 5 звёздочек в каждом ряду и 4 большие звёзды. сколько звёзд и звёздочек...
aadiiii1 aadiiii1  14.07.2019 14:10
Запиши возможные равенства. сколько их? обьясни.1) дес. 2ед. +8 ед. = дес. дес. -8 ед.=.2ед....
Капитошка1985 Капитошка1985  14.07.2019 14:10
Вырази ответ в крупных единицах. 38ц76кг+72ц24кг= если можно подробнее как получили ответ 120ц....
Fokus123123 Fokus123123  14.07.2019 14:10
Компьютерная игра состоит из трех этапов. костя набрал на первых двух этапах 780 очков, на третьем - в 3 раза меньше, чем на первом. сколько всего всего очков набрал...
Котик132457 Котик132457  14.07.2019 14:10
Из 12 кг слив масла можно получить 9 кг топлен.масла,а из 72 кг...
nocitronum nocitronum  14.07.2019 14:10
Длина коридора прямоугольной формы 6 м, а ширина на 2 м меньше 1) найди периметр этого коридора. 2) найди площадь этого коридора....

Популярные вопросы