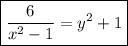Решить дифференциальное уравнение (xy^2 + x)dx - (y - x^2 y)dy=0, y=1; x=2
Другие вопросы по теме Математика
Популярные вопросы
- Впрямоугольном треугольнике проекция меньшего катета на гипотенузе равна 1см.а...
1 - Длина изгороди вокруг стадиона прямоугольной формы 2800м.определите площадь...
1 - Краткий пересказ 3-4 предложения вожждь краснокожих зарание большое...
1 - Краткое описание 3-4 предложения снегурочка -грим.зарание большое при большое...
2 - Влажность свежескошеной травы составляет 60% а влажность сена 20% . сколька...
1 - Уходом саша наполнил водой чайник объемом 15 л и поставил на вкл плиту в плотно...
1 - Втреугольнике авс угол с равен 90°,ас = 8,cos a=0,8. найдите длину стороны...
1 - X- множество букв в слове b- множество букв в слоге запишите множество х и...
3 - Рассчитайте стоимость погонного метра бруса сечением 150мм*150мм, если 1кубич.метр...
3 - Човен за 2 год руху за течією і 5 год руху проти течії пройшов 120 км. за 7...
2
Это уравнение с разделяющимися переменными
Получили общий интеграл дифференциального уравнения.
Найдем решение задачи Коши, подставляя начальные условия:
Частный интеграл: