1. Математика
  2. РЕШИТЬ ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ

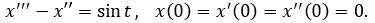
РЕШИТЬ ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ С ЗАДАННЫМИ НАЧАЛЬНЫМИ УСЛОВИЯМИ С ОПЕРАТОРОВ


РЕШИТЬ ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ С ЗАДАННЫМИ НАЧАЛЬНЫМИ УСЛОВИЯМИ С ОПЕРАТОРОВ

victorianna03 victorianna03    1   29.05.2020 07:26    0

Ответы
Август228 Август228  24.08.2020 22:46

x'''-x''=\sin t

Выполним преобразования Лапласа:

x(t)\rightarrow X(p)

x'(t)\rightarrow pX(p)-x(0)=pX(p)

x''(t)\rightarrow p^2X(p)-px(0)-x'(0)=p^2X(p)

x'''(t)\rightarrow p^3X(p)-p^2x(0)-px'(0)-x''(0)=p^3X(p)

\sin t\rightarrow\dfrac{1}{p^2+1}

Получим уравнение:

p^3X(p)-p^2X(p)=\dfrac{1}{p^2+1}

p^2(p-1)X(p)=\dfrac{1}{p^2+1}

X(p)=\dfrac{1}{p^2(p-1)(p^2+1)}

Разложим дробь, стоящую в правой части на составляющие:

\dfrac{1}{p^2(p-1)(p^2+1)}=\dfrac{Ap+B}{p^2} +\dfrac{C}{p-1}+\dfrac{Dp+E}{p^2+1}

1=(Ap+B)(p-1)(p^2+1) +Cp^2(p^2+1)+(Dp+E)p^2(p-1)

1=(Ap+B)(p^3-p^2+p-1) +Cp^2(p^2+1)+(Dp+E)(p^3-p^2)

1=\\=Ap^4-Ap^3+Ap^2-Ap+Bp^3-Bp^2+Bp-B+Cp^4+Cp^2+Dp^4-Dp^3+Ep^3-Ep^2

1=(A+C+D)p^4+(-A+B-D+E)p^3+(A-B+C-E)p^2+(-A+B)p-B

Условие равенства двух многочленов:

\begin{cases} A+C+D=0\\-A+B-D+E=0\\A-B+C-E=0\\-A+B=0\\-B=1\end{cases}

\Rightarrow\boxed{B=-1}

\begin{cases} A+C+D=0\\-A-1-D+E=0\\A+1+C-E=0\\-A-1=0\end{cases}

\Rightarrow\boxed{A=-1}

\begin{cases} -1+C+D=0\\1-1-D+E=0\\-1+1+C-E=0\end{cases}

\begin{cases} C+D=1\\D=E\\C=E\end{cases}

Заметим, что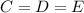 C=D=E. Подставляем в первое уравнение два других:

E+E=1

2E=1\Rightarrow \boxed{E=\dfrac{1}{2} }

C=E\Rightarrow \boxed{C=\dfrac{1}{2} }

D=E\Rightarrow \boxed{D=\dfrac{1}{2} }

Итак, дробь раскладывается на составляющие:

X(P)=\dfrac{-p-1}{p^2} +\dfrac{1}{2}\cdot\dfrac{1}{p-1}+\dfrac{1}{2}\cdot\dfrac{p+1}{p^2+1}

X(P)=-\dfrac{1}{p}-\dfrac{1}{p^2} +\dfrac{1}{2}\cdot\dfrac{1}{p-1}+\dfrac{1}{2}\cdot\dfrac{p}{p^2+1}+\dfrac{1}{2}\cdot\dfrac{1}{p^2+1}

Обратные преобразования Лапласа:

X(p)\rightarrow x(t)

\dfrac{1}{p}\rightarrow1

\dfrac{1}{p^2}\rightarrow t

\dfrac{1}{p-1}\rightarrow e^t

\dfrac{p}{p^2+1}\rightarrow\cos t

\dfrac{1}{p^2+1}\rightarrow\sin t

Получим искомую функцию:

x(t)=-1-t+\dfrac{1}{2}e^t+\dfrac{1}{2}\cos t+\dfrac{1}{2}\sin t

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
барбаришкин барбаришкин  30.03.2019 05:30
На спортивные соревнования п рибыло 120 участников,среди которых 36 мастеров спорти и 60 кандидатов в мастера спорта а) какую часть от общего числа участников состовляют...
311242aaa 311242aaa  30.03.2019 05:30
Трубу разрезали на 2 части 3,6м и 4,4м во сколько раз первая труба короче второй, сколько процентов всей трубы составляет от длины первой части...
violettaratonina violettaratonina  30.03.2019 05:30
Начертите отрезок, затем начертите отрезок, длина которого равна: 1/3; 3/4; 5/5; 7/5...
lublubkoba lublubkoba  30.03.2019 05:30
Периметр прямоугольника равен 16см,а его площадь 15см2. найдите длины сторон этогямоугольника....
Natalym2001 Natalym2001  30.03.2019 05:40
Фотоаппарат в футляре стоит 873 рубля. фотоаппарат стоит дороже футляра в 8 раз. сколько стоит фотоаппарат и сколько стоит футляр?...
hjccbyfoyf6ui hjccbyfoyf6ui  30.03.2019 05:40
Начертите отрезок, затем начертите отрезок, длина которого равна: 1/3; 3/4; 5/5; 7/5 поточнее я не поняла)...
Andriuy2003 Andriuy2003  30.03.2019 05:40
Придумайте название плаката на тему правильное...
darinashagaeva darinashagaeva  30.03.2019 05:40
Реши . мастер и его ученик работали 3 дня.в первый день они сделали 384 детали.это на 150 деталей меньше,чем во второй день,и в 2 раза больше,чем в третий.сколько деталей...
bogdan39 bogdan39  30.03.2019 05:40
Площадь поля 12 га, из них 8 га засеяно пшеницей. а) какая часть поля засеяна пшеницей? б) во сколько раз площадь всего поля больше площади участка, засеянного пшеницей?...
mariyapopova21 mariyapopova21  30.03.2019 05:40
17: 5=51: 15 перестановки членов пропорции составте три других верных пропорции...

Популярные вопросы