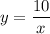Решить дифференциальное уравнение по условию
Другие вопросы по теме Математика
Популярные вопросы
- Найдите наибольшее и наименьшее значение функции на заданном промежутке...
2 - Темиртауские знаменитости эссе...
3 - Вычисли площадь прямоугольникаразными (пособами.4 см2 см7 см...
1 - Дайте определение деепричастия...
1 - 503. В геометрической прогрессии (b) найдите: а ) b2 b4,если b1=7,b5=56d)...
3 - Какие явления в жизни Франции свидетельствовали о развитии в стране капиталистических...
2 - Найди значение выражения 2m²n-4mn²+2n³ при m=135, n=35 ответ запиши в стандартном...
1 - Укажите предложение с причастным оборотом А) уж Верба,вся пушистая, раскинулась...
1 - .Азотосодержащие вещества образуются в результате полного разложения к ним...
2 - О Закінчіть розкладання на множники:(©-у степені) 1) 64х©6-0,027у©9= (4х©2)-(0,3у©3)©3=...
2
Найдите уравнение кривой, проходящей через точку M(2,5) и обладающей свойством, что отрезок любой ее касательной, заключенный между осями координат, делится пополам в точке касания.
По геометрическому смыслу производной
Пусть точка касания имеет координаты (x;y), тогда касательная отсекает на осях отрезки 2х и 2у. Угловой коэффициент касательной равен -y/x. Имеем дифференциальное уравнение: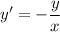 с начальным условием
с начальным условием 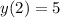
Данное дифференциальное уравнение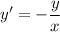 является уравнением с разделяющимися переменными.
является уравнением с разделяющимися переменными.
Подставляя начальное условие, мы найдем константу C
Искомое уравнение кривой: