1. Математика
  2. Решить дифференциальное

Решить дифференциальное уравнение

sashasevsova sashasevsova    1   14.09.2019 19:20    0

Ответы
tashbaeva201 tashbaeva201  07.10.2020 15:12

Обе дифференциальные уравнения являются уравнениями с разделяющимися переменными.

а)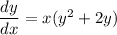 \dfrac{dy}{dx}=x(y^2+2y)

Разделяем переменные

\dfrac{dy}{y^2+2y}=xdx~~~\Rightarrow~~~ \displaystyle \int \dfrac{dy}{y^2+2y}=\int xdx~~\Rightarrow~~ \int\dfrac{dy}{(y+1)^2-1}=\int xdx\\ \\ \\ \dfrac{1}{2\cdot 1}\ln \bigg|\dfrac{y+1-1}{y+1+1}\bigg|=\dfrac{x^2}{2}+C\\ \\ \\ \boxed{\dfrac{1}{2}\ln \bigg|\dfrac{y}{y+2}\bigg|=\dfrac{x^2}{2}+C}

Получили общий интеграл и это есть ответ.

б)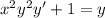 x^2y^2y'+1=y

x^2y^2y'=y-1~~~\Rightarrow~~~ \dfrac{dy}{dx}=\dfrac{y-1}{x^2y^2}~~~\Rightarrow~~ \displaystyle \int \dfrac{y^2}{y-1}dy=\int \dfrac{dx}{x^2}\\ \\ \\ \int\dfrac{y^2-1+1}{y-1}dy=-\dfrac{1}{x}+C~~~~\Rightarrow~~~ \int \dfrac{(y-1)(y+1)+1}{y-1}dy=-\dfrac{1}{x}+C\\ \\ \\ \int (y+1)dy+\int\dfrac{dy}{y-1}=-\dfrac{1}{x}+C\\ \\ \\ \dfrac{y^2}{2}+y+\ln|y-1|=-\dfrac{1}{x}+C

Получили общий интеграл.

ПОКАЗАТЬ ОТВЕТЫ
NotSmartBoy NotSmartBoy  07.10.2020 15:12

решение и ответ во вложении


Решить дифференциальное уравнение
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
XxШКОЛЬНИКxX XxШКОЛЬНИКxX  18.08.2019 17:10
Обчисли и зроби перевирку двома...
DEM0KRAT DEM0KRAT  18.08.2019 17:10
Выполните действия: а) (-56)+17= б) 42+(-29)= в) (-39)+(-57)= г) (-48)+81= д) 37+(-82)= е) (-68)+(-51)=...
karolina210 karolina210  18.08.2019 17:10
Решить 5 класс. велосипедист отправился догонять пешехода когда расстояние между ними было 24 км. скорость велос. 10км/ч, скорость пеш. 6км/ч. через сколько часов велосипедист догонит...
ndzandigiv ndzandigiv  18.08.2019 17:10
Икс разделить на 8 ровно 800 умножить на 10 плз...
banilchik26 banilchik26  18.08.2019 17:10
Найди правило, по которому составлены столбцы выражений.6+2,8-2,8-6,5+1,6-1,6-5,2+3,5-3,5-2. составь по томуже правелу выражение и найди их значение 6+3= 7+2= 5+4=...
hshdk hshdk  18.08.2019 17:10
Овощной киоск 35 килограмм яблок и 10 персиков когда несколько килограммов фруктов продали осталось 25 кг сколько килограммов фруктов продали...
Response21 Response21  18.08.2019 17:10
Тарелка стоит 32000р. сколько стоит 6 тарелок?...
Serzhantiko Serzhantiko  18.08.2019 17:10
Для подарка сыну отец купил 4 книги. все книги без первой стоят 84 руб., без второй 80, без третьей 76, без 4-й 72. какова стоимость каждой книги...
Марина19r Марина19r  18.08.2019 17:10
Периметры граней abcd, abb1a1 и add1a1 прямоугольного параллелепипеда abcda1b1d1 равны 20 м, 36 м и 32 м. найдите сумму длин всех его рёбер....
arsenkina2004 arsenkina2004  18.08.2019 17:10
Стекляную пластину размером 40см×60см обрезали на одинаковом расстоянии от каждой стороны.при этом ее площадь уменьшилась в 3 раза.найдите новые размеры пластины...

Популярные вопросы