1. Математика
  2. Решить дифференциальное уравнение

Решить дифференциальное уравнение (2x+1)dx-6ydy=0 и найти его частное решение, удовлетворяющее условиям: при x=1 y=2.

volodya13031 volodya13031    1   20.06.2020 23:49    0

Ответы
zagena09 zagena09  15.10.2020 14:36

y=\sqrt{\frac{x^{2}+x+10 }{3} }

Пошаговое объяснение:

(2x+1)dx-6ydy=0

(2x+1)dx=6ydy

\int\limits{(2x+1)} \, dx=\int\limits{(6y)}\, dy

x^{2} +x+C_{1} =3y^{2}+C_{2}

3y^{2} =x^{2} +x+C_{1}-C_{2} ; C_{1}-C_{2}=C

3y^{2} =x^{2} +x+C

y^{2} =\frac{x^{2} +x+C}{3}

\sqrt{y^{2}} =\sqrt{\frac{x^{2} +x+C}{3}}

|y| =\sqrt{\frac{x^{2} +x+C}{3}}

Отсюда получаем два решения:

y =\sqrt{\frac{x^{2} +x+C}{3}}}

y =-\sqrt{\frac{x^{2} +x+C}{3}}}

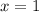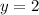Подставляем  в них x=1 и y=2  и решаем полученные уравнения относительно константы C:

2=\sqrt{\frac{1^{2} +1+C}{3} }

2^{2} =\sqrt{\frac{1^{2} +1+C}{3} } ^{2}

4=\frac{2+C}{3}

12=2+C

C=10 ; Тогда наша функция принимает вид:

y=\sqrt{\frac{x^{2}+x+10 }{3} }

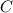Второе уравнение решений не имеет, поэтому ответ:

y=\sqrt{\frac{x^{2}+x+10 }{3} }

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
tt9692069 tt9692069  18.09.2019 09:00
Легкое тригонометрическое уравнение, sin x = - корень из 2 на 2...
Регина5111111 Регина5111111  18.09.2019 09:00
Найти число, если 7/11 его равны 4 целых 1/7...
SoloniyOgurets SoloniyOgurets  18.09.2019 09:00
Вычислите. 2 1/52* 26/49-11 5/11: 3 3/7...
янивановсергеевич янивановсергеевич  18.09.2019 09:00
Площадь прямоугольника равно 60м2,а его длина 12 м.чему равен его периметор?...
BEDmil00 BEDmil00  18.09.2019 09:00
Найдите остаток от деления 28 на 6. найдите неполное частное при делении 28 на 6. найдите остаток от деления 98 на 15. найдите неполное частное при делении 98 на 15. найдите...
dymovvla01928 dymovvla01928  18.09.2019 09:00
Нужно решить подробно : в двух бидонах 8,9л масла.в первом бидонести на 2,5л масла больше,чем во втором.сколько литров масла во втором бидоне?...
gravasamp gravasamp  18.09.2019 09:00
Разность на 60 меньше,чем вычитаемое.чему равно уменьшаемое если разность равна 150?...
nastushka208 nastushka208  18.09.2019 09:00
Вычисли: 1) 956×15+5216-74-84×17 2) 172×406+76960: 7×13 3) 75194-2759+45668: 7×13 4) 800000-645×402: 90×170 5) (30000: 40: 6+3782)×23 6) 56760-(345×74-25530)×36 7) 60300:...
valenkov05 valenkov05  18.09.2019 09:00
(25 б)составьте числовое выражение и вычислите его значение: 1)к числу 16,53 прибавить сумму чисел -19,8 и 2,19 2)к сумме чисел -2.2/3 и -5.1/4 прибавить число 3.2/5 3)к сумме...
MilkaV MilkaV  18.09.2019 09:00
Сумма 2 чисел равна 520 а их отношение равно 4 найдите эти числа проверьте ответ...

Популярные вопросы