решить дифференциальное уравнение
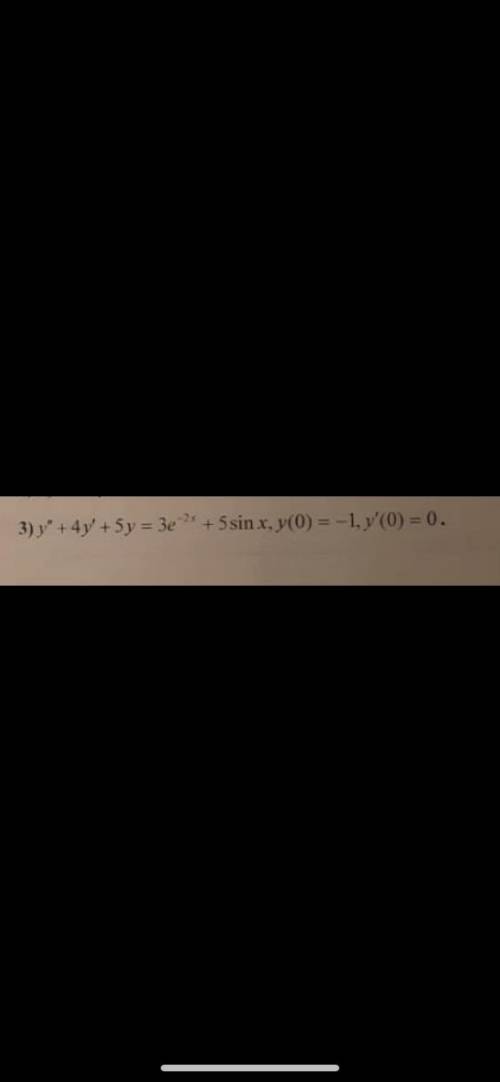
Другие вопросы по теме Математика
Популярные вопросы
- Гетерозиготный желтый морщинистый горох скрещен с зелёным,гетерозиготным...
1 - Найти площадь треугольника стороны которого равны 4√3 и 12 , а угол...
3 - Что такое фаза? привидите примеры веществ,находящихся в различных фазах...
1 - Длина цветника прямоугольной формы равна 20 метров ширина 5 метров...
3 - Существительные с суффиксом-ок- написание суффикса-ок- после шипящих...
3 - Скакого вещества можно водные растворы метанола и глецирина?...
1 - Охарактеризуй стихотворение «и. и. пущину»...
3 - Краткий пересказ рассказа михаила зощенко гроза...
1 - Запиши три десяткових дроби,кожний з яких менший від 8.52 і більший...
2 - Из городов а и в находяшихся на расстоянии 275 км.друг от друга вышли...
2
1. ОЛДУ:
2. Подбираем у с неопределенными коэффициентми
В НЛДУ:
Получаем
Общее решение:
Частное решение