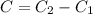Решить диф. ур.
(dy/dx)=(xy*cos(x))/(1+y^2)
Другие вопросы по теме Математика
Популярные вопросы
- Втреугольнике авс два угла острые. тогда третий угол треугольника может...
2 - Докажите ,что выражение 5•2^48-3•2^47-4•2^45 кратно 24 где знак ^ это...
2 - Для чего нужны условные обозначение в учебнике риторики? 4 ! буду !...
2 - Закончите схемы реакций: a) mgso4+na2co3- б) ba+s- в) caco3+co2+h2o-...
3 - Сколько в слове уши слогов? 2 или 1?...
3 - Cкажите ! как разобрать слово метро...
3 - Укажи значение выражения а*500,если а=60...
3 - Вцилиндрическом сосуде уровень жидкости достигает 12 см . на какой высоте...
2 - Определи закономерность букв в каждом квадрате и дописать букву и объяснить...
1 - Как разложить пример по формуле (2х+5) во второй степене. нужно...
1
-- уравнение с разделяющимися переменными.
Разделим переменные:
-- уравнение с разделенными переменными.
Проинтегрируем обе части последнего уравнения:
Вычислим записанные интегралы:
Получаем
- общий интеграл данного уравнения, где