1. Математика
  2. Решить дано двузначное

Решить дано двузначное натуральное число, у которого число единиц на 1 больше числа десятков. известно,что сумма квадратов его цифр в 5 раз больше увеличенного на 2 числа его десятков. найти это число

kamilla198 kamilla198    2   09.06.2019 21:40    0

Ответы
ДарьяРэя ДарьяРэя  08.07.2020 14:08
Пусть число записывается как 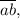 \overline{ab},  где а - число десятков (цифра),  в - число единиц (цифра).

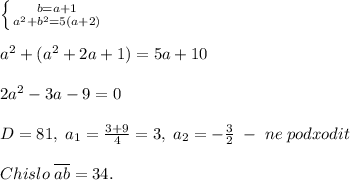
\left \{ {{b=a+1} \atop {a^2+b^2=5(a+2)}} \right. \\\\a^2+(a^2+2a+1)=5a+10\\\\2a^2-3a-9=0\\\\D=81,\; a_1=\frac{3+9}{4}=3,\; a_2=-\frac{3}{2}\; -\; ne\; podxodit\\\\Chislo\; \overline{ab}=34.
ПОКАЗАТЬ ОТВЕТЫ
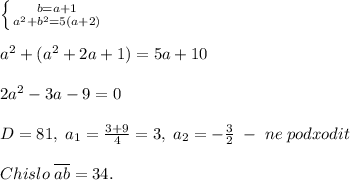
Другие вопросы по теме Математика
DanilKrut11 DanilKrut11  19.07.2019 17:10
Туристы проехали одеу вторую всего пути на поезде.0,3 пути на автобусе, а остальную часть пути проплыли на катере ? запишите в порядке убывания расстояние,пройдённые...
43446764949 43446764949  19.07.2019 17:10
Запиши множину чисел більші за 13 і менші від 20...
Алеся1111115 Алеся1111115  19.07.2019 17:10
Условие из 42 участников конкурса 6 человек стали призерами...
Nik228tyto4ki Nik228tyto4ki  19.07.2019 17:10
Первой клетке 8 кроликов ,во второй -на 2 кролика меньше ,чем в первой ,а в третьей на 3 кролика больше ,чем во второй ,сколько кроликов в третьей клетке...
ask52 ask52  19.07.2019 17:10
Укажи правильное значение суммы чисел 368 и 469...
kotik12345566 kotik12345566  19.07.2019 17:10
Хоккейный тренер олимпийской сборной, приехавшей на соревнования в количестве 40 человек, заявляет на отборный матч состав из 2-х вратарей и шести игровых пятерок....
асема2005 асема2005  19.07.2019 17:10
Можно ли,имея лишь 2 сосуда обьём которых 7 л и 5 л набрать из водопроводного крана 4 л воды?...
Лиза878897897 Лиза878897897  19.07.2019 17:10
Грибы при сушке теряют 90% своей массы. из какого количества свежих грибов было получено 5 кг сушенных?...
оркп оркп  19.07.2019 17:10
Найдите большой корень уравнения 0,01y² - 4= 0...
20070706 20070706  19.07.2019 17:10
Масса овцы 72 кг,а масса ягнёнка 18кг.во сколько раз масса овцы больше массы ягнёнка? на сколько кг масса ягнёнка меньше массы офцы?...

Популярные вопросы