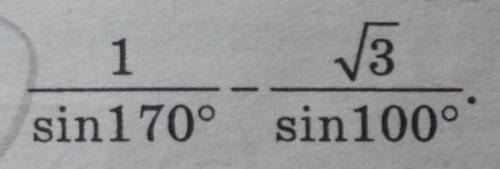
Математика: Решить через формулы по тригонометрии)

Решить через формулы по тригонометрии)

Ответы

katy244 30.03.2021 13:31

Пошаговое объяснение:

Сначала приведём синусы к одному углу:

$\sin{170^{\circ}} = \sin{\left(180^{\circ} - 10^{\circ}\right)} = \sin{10^{\circ}}$

$\sin{100^{\circ}} = \sin{\left(90^{\circ} + 10^{\circ}\right)} = \cos{10^{\circ}}$

Теперь сложим дроби

$\dfrac{1}{\sin{10^{\circ}}} - \dfrac{\sqrt{3}}{\cos{10^{\circ}}} = \dfrac{\cos{10^{\circ}} - \sqrt{3} \sin{10^{\circ}}}{\sin{10^{\circ}} \cos{10^{\circ}}}$

В числителе наклёвывается синус разности (или косинус суммы). Корень из трёх не является словарным косинусом (и в принципе косинусом), но вот поделённый пополам -- это косинус тридцати градусов. Поэтому поделим числитель и знаменатель на два

$\dfrac{\cos{10^{\circ}} - \sqrt{3} \sin{10^{\circ}}}{\sin{10^{\circ}} \cos{10^{\circ}}} = \dfrac{\dfrac{1}{2}\cos{10^{\circ}} - \dfrac{\sqrt{3}}{2} \sin{10^{\circ}}}{\dfrac{1}{2}\sin{10^{\circ}} \cos{10^{\circ}}}$

В числителе получили синус разности, в знаменателе синус двойного угла, множитель 2 для которого нужно вручную вытащить из 1/2:

$\dfrac{\sin{30^{\circ}}\cos{10^{\circ}} - \cos{30^{\circ}} \sin{10^{\circ}}}{\dfrac{1}{2}\sin{10^{\circ}} \cos{10^{\circ}}} = \dfrac{\sin{\left( 30^{\circ} - 10^{\circ} \right)}}{\dfrac{1}{4} \cdot 2\sin{10^{\circ}} \cos{10^{\circ}}} = \dfrac{\sin{20^{\circ}}}{\dfrac{1}{4} \cdot \sin{20^{\circ}}} = 4.$