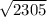решить буду очень благодарен.
Другие вопросы по теме Математика
Популярные вопросы
- Какое сочинение написать про город абакан...
2 - :3 запиши, какие числа нужно подавать на вход чтобы получать числа: 5,...
1 - При использовании автоматической линии по упаковки продуктов производительность...
3 - Найдите больший угол остроугольного треугольника, если две его стороны...
2 - Укажите слово в котором есть звонкий согласный звук не имеющий пары по...
3 - Посмотри программу новостей и расскажи о государственных делах президента...
3 - Программирование, 10 класс pascal abc необходимо написать код к (как можно...
1 - Надо на тему профессия повор взорание...
3 - Сравните стороны треугольника авс, если угол а угла в угла с...
3 - Михаил купил справочник по ,потратил на него 45% имевших него денег.сколько...
3
x1 = -2 - 3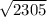
x2 = -2 + 3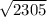
Пошаговое объяснение:
log12 (x^2 + 4x - 5) = -4
ОДЗ: x^2 + 4x - 5 > 0
Рассмотрим функционально:
y = x^2 + 4x - 5
Находим нули функции:
x^2 + 4x - 5 = 0
x1 = -5
x2 = 1
Начертив числовую ось Ox и отметив на ней эти точки и промежутки возрастания/убывания, получим, что данное уравнение возрастает при x э (-Б; -5) ∪ (1; +Б) (символ э должен быть отзеркален, но я не нашла такого символа, чтобы вставить извинить за неточности в решении...)
ОДЗ: x э (-Б; -5) ∪ (1; +Б)
log12 (x^2 + 4x - 5) = -4
x^2 + 4x - 5 = 12^4
x^2 + 4x - 5 = 20736
x^2 + 4x - 5 - 20736 = 0
x^2 + 4x - 20741 = 0
x1 = -2 - 3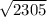
x2 = -2 + 3