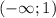Решить , а то за лето подзабыл 1.решите неравенство f'(x)> 0 a)f(x)=-8x^2-2x+1 b)f(x)=1+x-6x^2 c)f(x)=(x^3/)+2 (поставил скобки,чтобы вы не запутались дробью,а так там такого нет) d)f(x)=)/3)- 1/2x^2+6/7 (не обязательно конечно,но если можно то с
объяснениями)
Другие вопросы по теме Математика
Популярные вопросы
- егер мен ертеги кеипкер болсам эссе базу...
3 - Какие файлы в APK отвечают за интерфейс программы. ...
3 - Представим в виде степине выражения : x10:x7=...
2 - Что вы можете сказать об Актеоне? Какой он? Какова основная мысль мифа?...
3 - докажите,что графики уравнений x-y=4 и y=5-5x+x^2 пересекаются только в одной...
2 - Үндестік заңына бағынбайтын сөз асқазан, түйеқұс қосаяқ...
1 - как природно-климатические условия повлияли на занятия жителей государства, в...
2 - это не трудно просто у меня времени не хватает желательно чтобы побольше написать...
3 - Представьте в виде степени выражения:y13:y8...
1 - Берілген нысандарды екі бағанға бөліп орналастыр.Өз таңдауыңды дәлелде ...
1
a)f(x)=-8x^2-2x+1
f'(x)=-8*2x-2*1=-16x-2
-16x-2>0
-16x>2
x<-2/16
x<-1/8
b)f(x)=1+x-6x^2
f'(x)=1-6*2x=1-12x
1-12x>0
-12x>-1
12x<1
x<1/12
c)f(x)=(x^3/3)-(x^2)+2
f'(x)=1/3 * 3x^2 -2*x=x^2 - 2x
x^2 - 2x>0
x^2 - 2x =0
x(x-2)=0
x=0 x=2
Чертим координатную прямую и отмечаем точки, расставляем знаки.
___+______-______+_____
0 2
Решением неравенства является промежуток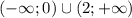
d)f(x)=((-x^3)/3)- 1/2x^2+6/7
f'(x)=-1/3 * 3x^2 - 1/2 * (-2)* 1/x^3 =-x^2 +1/x^3
-x^2 + 1/x^3 >0
Домножим на x^3:
-x^5 +1>0
-x^5>-1
x^5 < 1
x<1
Решением будет являться промежуток