решить) a,b>0 натуральные числа
Доказать равенство:
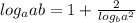
Другие вопросы по теме Математика
Популярные вопросы
- Что такое пдд,па-д,гра-па,тру-а,гра-па в музыке ()...
1 - Запишіть: добрим, привітним, байдужим, спокійним, чи жорстоким...
1 - Какое выражение нужно добавить к (a-b) в квадрате чтобы получить...
1 - Записать пять несклоняемых имен существительных....
1 - Разобрать морфологический разбор слова пчёлы зарание !...
2 - Как правильно шить кретиком что бы сзади не было узелков? ( это...
3 - 16. лекарственная ромашка теряет при сушке 84 % массы. сколько...
1 - ~1. что образует единство музыкального произведения? 2. назовите...
1 - Вкакой пословице говорится что в чём-либо человек изобретателен?...
3 - Найдите средний арифмитический корень у 0.01 и 1.2...
2
Рассмотрим правую часть
Для доказательства использовались следующие свойства: