Решить 17
докажите что при любом натуральном n значении выражения

Ответы

karina809 07.10.2020 00:50

Здесь будем пользоваться свойством степеней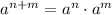 $a^{n+m}=a^n\cdot a^m$

$11^{n+4}-11^n=11^n\cdot 11^4-11^n=11^n(11^4-1)=11^n(11^2-1)(11^2+1)=\\ \\ \\ =11^n\cdot (121-1)\cdot (121+1)=11^n\cdot 120\cdot122$

Один из сомножителей делится на 61, значит и исходное выражение делится на 61.

$7^{n+3}+7^n=7^n\cdot 7^3+7^n=7^n\cdot(7^3+1)=7^n\cdot(343+1)=7^n\cdot 344$

Множитель 344 делится на 43, т.е. исходное выражение делится на 43

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Математика

maks737 23.12.2020 07:41

Выполните действия 5/21 + 2/3...

bodleva06 23.12.2020 07:41

Viking012345 23.12.2020 07:42

lara1906 23.12.2020 07:42

лучшая40 23.12.2020 07:43

Light111111 23.12.2020 07:43

Serlous 23.12.2020 07:43

Соня135135 23.12.2020 07:43

решить! Понимаете, это очень...

Sabziro18 20.05.2020 07:31

Построй квадрат со стороной 50мм...

никанана 20.05.2020 07:31