Решить, ! 1) найти наклонную асимптоту у=kx+b графика функции f(x)=√4x^2+3x-5 при х стремящемуся к + ∞. в ответе укажите k+b 2) напишите уравнение касательной y=kx+b к рафику функции f(x)=-x^3-2x^2+x в точке а=2. в ответе укажите k+b
3)используя формулу маклорена для f(x)=е^x до 2-го порядка, вычислите приближенно e^-0.1 4)вычислите площадь фигуры, ограниченной прямйой у=-х+14 и гиперболой у=65/(х+4) 5) найдите производную функции f(x,y)= (2x+2y)/(-x-3y) в точке а(2,-1)
в направлении вектора е=(-5,1) 6)исследуйте функцию на локальный экстремум f(x,y)=-5x^2+y^2-4xy+26x-4y. в ответе укажите сумму координат точек экстремума
Другие вопросы по теме Математика
Популярные вопросы
- Составь 4 предложения про ёлку применяя слова: лиса,ёжик.мишка,ёлка,шишка,грибы,иголки,шарики,зелёные,острые...
2 - Загадка про інтернет у віршованій або прозовій формі...
3 - Утани было 5 конфет,у маши столько же,а у анжелы в 2 раза больше чем...
3 - 4. they went the disco last night. at, in, on, to 5. how tables and chairs...
3 - Какое сложное(в кором два коня и соединительная буква о , и е) слово...
1 - 1. выберите верный вариант ответа: а) право— совокупность правил поведения,...
3 - Обьяснение слов нактюрн полонез мазурка вальс прилюдие этюд...
2 - За 777 рублей некто купил узбечку седло лошадь и карета сколько стоила...
2 - Кому было адресовано стихотворение тютчева к.б.?...
2 - Скакой скоростью должен двигаться мототоцикл по выпуклому участку дороги...
3
1)
ответ: b+k=2+3/4=11/4
2) y=f(a)+f'(a)(x-a)
f(x)=-x³-2x²+x f(2)=-14
f'(x)=-3x²-4x+1
f'(2)=-19
y=-19x+24
ответ: k+b=-19+24=5
3) f(x)=e^x
4) Найдем точки пересечения графиков
65/(x+4)=14-x
-x²+10x-9=0
x₁=1 x₂=9
5)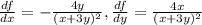
Направляющий вектор {-5/√26, 1/√26}
ответ: 4(-5/√26)-4/√26 = -24/√26