Реши уравнение: })
Другие вопросы по теме Математика
Популярные вопросы
- Составить две на движение и решить их...
2 - 12 ! определите черты своего характера(какие вы считаете характерны...
1 - Решить систему уравнений y=x-1, x^2+y=1...
1 - Очем говорится в стихотворении а. фета какая грусть, конец аллеи...
2 - Какой будет потенциальная энергия мальчика массой 40кг по отношению...
2 - Основные герои в сказке мальчик с пальчик...
1 - Сочинение на тему осторожно грипп! что так сложно что ли люди не несите...
2 - По языку разобрать по членам предложения что такое наводнение? это...
3 - Катеты прямоугольного треугольника равны 3см и 4см. обьем какого конуса...
3 - Сколько потребуется голубой эмали для покраски потолка в комнате длинной...
1
Приведём всё к общему знаменателю.
При х=0 и a= -2 выражение не существует.
У нас х ≠ 0 и при этом х=f(a), то есть f(a) ≠ 0
Пройдёмся по ограничениям.
При х=0 и а= -2 выражение не определено (суть в том, что нельзя сказать нет решений, выражение просто не существует).
При a= -3: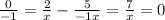
Как видно решений нет.
При а= 0.5: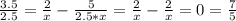
выражения с х сокращаются и остаётся только 7/5 = 0 как видно это не верное тождество, значит для всех х, при а=0.5 - решений нет.
Комментарий к ответу: в первой строчке х принадлежит пустому множеству (нет решений), во второй строчке а принадлежит всем действительным числам, кроме -3;-2 и 0.5