Реши : лодка может пройти расстояние между двумя посёлками,стоящим на берегу реки,за 4 часа 20 минут против течения реки и за 2 часа 10 минут по течению.скорость течения реки равна 1,5 км/час.найди собственную скорость лодки и расстояние между посёлками.
Другие вопросы по теме Математика
Популярные вопросы
- Запиши слова в два столбика: 1) слово с мягким знаком; 2)слова без мягкого...
1 - Подскажите как делать. выполни разностное и кратное сравнения площадей...
3 - 1. вычислите: а) 1 + 3/8 б) 1/4 + 1/8 в)1/10 + 1/15 г) 1/2 + 2 /3 д) 1...
3 - Вычесли площадь прямоугольника сдлинами сторон 6 см и 5 см...
2 - С. в двух кусках поровну ткани. после того как от первого куска продали...
3 - Грамотическая основа в прдложени на лесной поляне вмден могучий дуб...
1 - Реши уравнение а)15x=0,15 в)3а+ 8а=1,87 д) 2t+5t+3,18=25,3...
1 - Одна открытка, 2 одинаковых конверта и 3 одинаковые марки стоят 38 рублей....
3 - Решил . вычисли и запеши ответ. в первый день туристы. были в пути 10 часов...
3 - Что сделал олег? игорь? ольга? святослав, владимир 1, ярослав мудрый, владимир...
2
Пусть собственная скорость лодки равна x км/ч. Тогда скорость по течению равна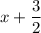 км/ч, а против —
км/ч, а против — 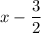 км/ч.
км/ч.
По течению лодка плыла 2 ч 10 мин =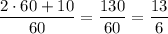 ч. Расстояние, которое она проплыла по течению, равно
ч. Расстояние, которое она проплыла по течению, равно 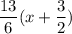 км.
км.
Против течения лодка плыла 4 ч 20 мин =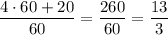 ч. Расстояние, которое она проплыла против течения, равно
ч. Расстояние, которое она проплыла против течения, равно 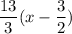 км.
км.
Так как оба расстояния – это одно и то же, составим уравнение:
4,5 км/ч — собственная скорость лодки. Чтобы найти расстояние, достаточно подставить это в одно из уравнений расстояния. Подставим в тот случай, когда лодка плыла против течения:
ответ: 4,5 км/ч, 13 км.
4,5 км/ч, 13 км.
Пошаговое объяснение:
Пусть скорость лодки равна x км/ч, тогда скорость по течению
x+1,5 км/ч, а против течения x-1,5 км/ч.
Время 4 ч 20 мин = 4 1/3 = 13/3 часа, 2 ч 10 мин = 2 1/6 = 13/6 часа.
Расстояние по течению: (x+1,5)*13/6 км.
Расстояние против течения: (x-1,5)*13/3 км.
И эти расстояния одинаковы, так как это одно и тоже.
S = (x+1,5)*13/6 = (x-1,5)*13/3
(x+1,5)/6 = (x-1,5)/3
(x+1,5) = 2(x-1,5)
x + 1,5 = 2x - 3
3 + 1,5 = 2x - x
x = 4,5 км/ч - это собственная скорость лодки
S = (x+1,5)*13/6 = (4,5 + 1,5)*13/6 = 6*13/6 = 13 км - это расстояние.