1. Математика
  2. Решение задачи Коши для дифференциального

Решение задачи Коши для дифференциального уравнения
второго порядка
y''-9y=9x, y(0)=0,y'(0)=0

katyar980 katyar980    1   07.03.2020 01:04    0

Ответы
abi182 abi182  11.10.2020 20:36

Решаем соответствующее однородное диф. уравнение

y'' - 9y = 0

Переходим к характеристическому уравнению

k^2-9=0\\ k=\pm3

Общее решение линейного однородного диф. уравнения

Yo.o =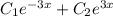 C_1e^{-3x}+C_2e^{3x}

Рассмотрим правую часть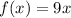 f(x)=9x. Частное решение будем искать в виде : Yч.н. =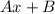 Ax+B

y'=A\\ y''=0

-9(Ax+B)=9x\\ -9Ax-9B=9x

Приравнивая коэффициент при степени x, мы получим

-9A = 9 откуда A = -1

-9B = 0 откуда B = 0

Следовательно, Yч.н. = -x

Y = Yo.o. + Yч.н. =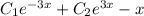 C_1e^{-3x}+C_2e^{3x}-x - общее решение линейного неоднородного дифференциального уравнения.

y'=-3C_1e^{-3x}+3C_2e^{3x}-1

Найдём теперь задачу Коши, подставив начальные условия

\displaystyle \left \{ {{C_1+C_2=0} \atop {-3C_1+3C_2-1=0}} \right. ~~\Rightarrow~~\left \{ {{C_1=-\dfrac{1}{6}} \atop {C_2=\dfrac{1}{6}}} \right.

\boxed{y=-\dfrac{1}{6}e^{-3x}+\dfrac{1}{6}e^{3x}-x}

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
Łųçů Łųçů  19.04.2021 11:59
Задание 4.По графику перемещения равномерно движущегося тела определите: а) перемещение тела за 5 ч; б) скорость тела...
89043780617 89043780617  19.04.2021 11:59
ответьте буду очень благодарен Выразите переменную у через переменную х из линейного уравнения...
минкп минкп  19.04.2021 11:59
, 2 1/2y - 1,27 = 3/4y - 4,77...
maksimfomin2020 maksimfomin2020  19.04.2021 11:59
В библиотеку привезли учебники по математике и чтению, всего 147 учебников. Учебники по чтениюпоставили на з полки, по 25 учебников на каждую.Учебники математике поставили поровну2...
дико64 дико64  19.04.2021 11:59
ПОСТРОЙТЕ НА ОДНОЙ КООРДИНАТНОЙ ПЛОСКОСТИ 2 ГРАФИКА ​...
gugem gugem  19.04.2021 11:59
Заполни магический квадрат.​...
Хшж Хшж  19.04.2021 11:58
Тема КоэффициентКарточка 11) (2x – Зу) — (5х + 2у);2) –(p — Зq) + (4q – 2р);3) (-x+ Sy) – (-х – Зу);4) (-3z+y) + (-16z – бу);5)-(-3х – 5c) — (3c + 8х).​...
polinamimi2006 polinamimi2006  19.04.2021 11:58
А) 4 менен 2нин тийиндисине 19ду кош б) 40тан 6 менен 3тун тийиндисине кемит в) 5 менен 3тун кобойтундусунон 8 менен 4тун тийиндисин кемит. ​...
coolmeen coolmeen  19.04.2021 11:58
Знайти похідну 1) t(x)=x-2/x⁵​...
partybally partybally  19.04.2021 11:58
Решите уравнение:(1,21-3х):0,04+6,4=80...

Популярные вопросы