Решение тригонометрических уравнений
2cos2x-5cosx+3=0
Другие вопросы по теме Математика
Популярные вопросы
- Написати твір на тему чому й до цього часу нас чарують пісні марусі чурайна...
3 - Составьте сначала правильно формулы веществ, вместо знаков вопроса вставьте...
3 - Каким целям служило европейское равновесие ?...
1 - Основа та корінь слова чоло, очолити, очільник, знечулити, чумакувати,...
1 - Написать по казахскому языку, правильно...
1 - Какая сумма точек на гранях будет повторяться наиболее часто при бесконечно...
2 - Мини-сочинение по произведению бедная лиза в сочинении ответить на вопросы:...
2 - Как на конарденатной плоскости можно написать имя даша 32...
2 - Ть треба пояснити правопис за правилами: 1. ламається (перша а) 2. вечірняя...
1 - Ағзалардың бірлестігі дегеніміз не?...
3
Воспользуемся формулой косинуса двойного угла:
Решаем уравнение относительно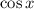 . Заметим, что сумма коэффициентов равна 0. Значит:
. Заметим, что сумма коэффициентов равна 0. Значит: