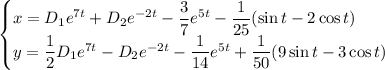Решение систем линейных неоднородных дифференциальных уравнений с постоянными коэффициентами методом вариации постоянных.
Другие вопросы по теме Математика
Популярные вопросы
- Мини сочинение по сказке Левша по плану.1)Тема 2)Идея3)Отзыв4)Своё...
2 - Что под цифрами, сосна обыкновенная...
3 - решить . Заранее огромное....
2 - С . Задача Выборы в США Выборы в США Как известно, в США президент...
1 - Смесь безводных сульфатов железа(II), кобальта(II) и никеля(II),...
2 - CONDITIONAL MOOD БУДЬ ЛАСОЧКА! 5. Краще б день був не таким нудним....
2 - 1. В калориметре находится в тепловом равновесии лед и вода одинаковых...
3 - Задача 1 В саду росло 208 фруктовых деревьев.яблонь и слив было...
3 - Сколько корней имеет уравнение x^3=sin3x?...
1 - Мини сочинение по сказке Левша по плану. 1)Тема 2)Идея 3)Отзыв 4)Своё...
1
Полное решение в прикрепленном файле, здесь некоторые подробные расчеты пропущены, так как слишком длинное решение не хочет добавляться.
Продифференцируем первое уравнение:
Подставим выражение для y' из второго уравнения:
От получившегося уравнения отнимем первое уравнение системы:
Решим однородное уравнение, соответствующее данному неоднородному:
Составим характеристическое уравнение:
Предположим, что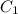 и
и 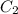 не константы, а некоторые функции
не константы, а некоторые функции 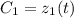 и
и 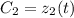 .
.
Найдем первую производную:
Пусть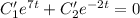 . Тогда:
. Тогда:
Найдем вторую производную:
Подставим значения функции и производных в уравнение относительно х:
Добавим к полученному уравнению условие, заданное на этапе нахождения первое производной:
Из первого уравнения выразим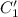 :
:
Подставим во второе уравнение:
Найдем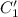 :
:
Необходимо проинтегрировать выражения для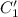 и
и 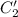 . Для этого предварительно вычислим следующие циклические интегралы, пользуясь формулой интегрирования по частям:
. Для этого предварительно вычислим следующие циклические интегралы, пользуясь формулой интегрирования по частям:
1)
2)
3)
4)
Интегрируем выражение для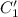 :
:
Интегрируем выражение для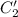 :
:
Подставляем выражения для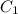 и
и 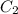 в решение:
в решение:
Найдем производную:
Из первого уравнения исходной системы выразим у:
Подставляем выражения для х и х':
ответ: