1. Математика
  2. Решение , однородные дифференциальные

Решение , однородные дифференциальные уравнения

Lina300333 Lina300333    2   04.01.2020 13:11    0

Ответы
Женя8а Женя8а  10.10.2020 23:49

Перепишем уравнение так: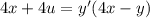 4x+4u=y'(4x-y)

Данное дифференциальное уравнение является однородным. Для него осуществляется замена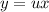 y=ux, тогда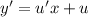 y'=u'x+u

4x+4ux=(u'x+u)(4x-ux)\\ \\ x=0;~~~ 4+4u=(u'x+u)(4-u)\\ \\ 4+4u=4u'x+4u-u'ux-u^2\\ \\ u'x(4-u)=u^2+4

Пришли к дифференциальному уравнению с разделяющимися переменными

\dfrac{du}{dx}=\dfrac{u^2+4}{x(4-u)}~~~~\Rightarrow~~~~\dfrac{(4-u)du}{u^2+4}=\dfrac{dx}{x}~~~\Rightarrow~~~ \displaystyle \int \dfrac{(4-u)du}{u^2+4}=\int \dfrac{dx}{x}\\\\ \\ \int \dfrac{4du}{u^2+4}-\dfrac{1}{2}\int \dfrac{d(u^2+4)}{u^2+4}=\int \dfrac{dx}{x}\\ \\ \\ 4\cdot \dfrac{1}{2}{\rm arctg}\, \dfrac{u}{2}-\dfrac{1}{2}\ln \big|u^2+4\big|=\ln |x|+C

Выполнив обратную замену получим

2{\rm arctg}\, \dfrac{y}{2x}-\dfrac{1}{2}\ln \bigg|\dfrac{y^2}{x^2}+4\bigg|=\ln |x|+C — общий интеграл

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
necoshevcom necoshevcom  04.05.2019 11:03
Запиши сумму числа 16.чтобы два числа были однозначными.что это за числа? два примера....
trostsnska trostsnska  04.05.2019 11:03
постройте график функции у = – 3,5х – 1. найдите координаты точки, абсцисса и ордината которой а) равны, б) отличаются друг от друга в 2 раза...
Victor111111111 Victor111111111  04.05.2019 11:06
Решить пример по действиям.729×(5-3)+(27÷3+6)-48: (2×3)=...
annakivilyova annakivilyova  04.05.2019 11:07
Школьники за три дня собрали 560 кг помидоров. в первый день они собрали 35% всех помидоров, что составило 7/8 количества помидоров, которые собрали на второй день. сколько помидоров...
Георгий161 Георгий161  04.05.2019 11:10
Не могли бы вы мне в решение одной ! ссылка на картинку...
reginailt reginailt  04.05.2019 09:18
Нужно, заранее ) в результате наблюдений за случайной величиной x получена выборка объема n=50 . а) определить для выборки основной промежуток [a,b] , количество интервалов распределения...
YanaTarabakina YanaTarabakina  04.05.2019 09:21
Найдите область определения функции y=lg 2x+1/x-1...
aiha4567 aiha4567  04.05.2019 09:21
Расположите числа корень 52; 4корень5 и 8,3 в порядке возрастания. ответ обоснуйте...
annagrits66 annagrits66  04.05.2019 09:23
Составьте систему линейных уравнений с двумя переменными у которых решения будет x=6; y=1​...
mordecaill122 mordecaill122  04.05.2019 09:27
Всегото 1 и с обьяснением как вы нашли...

Популярные вопросы