РЕБЯТА, ОЧЕНЬ кто может РЕШИТЬ, можно ответ, буду очень БЛАГОДАРНА

Відповідь:

ΔABD рівнобедрений. P ≈ 32,4 см

Покрокове пояснення:

OA = OD; BO⊥AD ⇒ OB - медіана і висота ΔABD. Отже ΔABD - рівнобедрений.

OA = AD/2 = 14/2 = 7 см

Оскільки  ΔAOB - прямокутний, то за теоремою Піфагора

AB^2 = OA^2 + OB^2

AB^2 = 7^2 + 6^2 = 49 + 36 = 85

AB =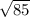

DB = AB =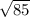

P = AD + 2*AB = 14 + 2 *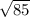 ≈ 14 + 2 * 9,2

P ≈ 32,4