Ребят с этим? с решением(( ABC -равносторонний треугольник (1 фигура)
И вторая картинка задание :
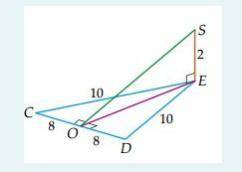
Точка S лежит вне плоскости равностороннего треугольника CDE. Известно, что SE перпендикулярный треугольник C D E, CE = ED = 10 см,
CD = 16 см, SE = 2 см. Вычислите расстояние от точки S до линии CD.
пож оч надо
Другие вопросы по теме Математика
Популярные вопросы
- Задача на Python Квадранты Дано число n. Создайте массив размером n×n и заполните...
1 - Знайти значення похідної функції у= 2sinx в точці х0 = 2π варіанти відповідей...
3 - Скільки існує звичайних дробів, чисельник і знаменик яких - різн числа, не більші...
2 - При якому значенні к графік функції у = к х - 8 проходить через точку А(-2; 10)....
2 - Виберіть із запропонованих термінів зайвий та коротко обґрунтуйте свій вибір:...
2 - План до твору Ольги Кобилянскої Фантазія експромт Зарание большое...
2 - Решите На листочке Геометрия 8кл....
3 - Одна з двоих чисел в 1,8 раз більше за друге.Знайди ці числа,якщо їхня сума дорівнює...
3 - Решить задачу: в лесу в рядочек выросли 6 грибов. Расстояние между каждыми соседними...
3 - Дві бригади робітників виготовили у січні 900 деталей. У лютому перша бригада...
2
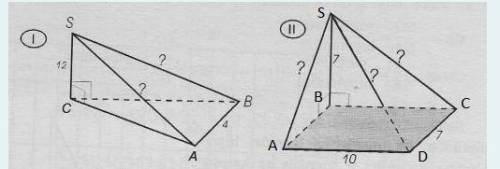
№1
Дано:
∆АВС – равносторонний,
SC=12,
AB=4,
Углы SCA и SCB – прямые.
Найти: SA, SB
Так как ∆ABC – равносторонний по условию, то АС=ВС=АВ=4.
Углы SCA и SCB – прямые по условию, тогда ∆SCA u ∆SCB – прямоугольные.
По теореме Пифагора в ∆SCA:
SA²=SC²+AC²
SA²=12²+4²
По теореме Пифагора в ∆SCB:
SB²=SC²+BC²
SB²=12²+4²
ответ: 4√10.
№2
Дано:
∆АВС – равнобедренный с основанием CD (не равносторонний так как CE≠CD),
CE=ED=10 см,
CD=16 см,
SE=2 см,
Угол SEO=90°,
ЕО – высота ∆АВС.
Найти: SO
Высота равнобедренного треугольника, проведенная к основанию, так же является медианой.
Следовательно ЕО – медиана, значит CO=DO=0,5CD=16*0,5=8 см.
Так как ЕО – высота, то угол ЕОС=90°, тогда ∆ЕОС – прямоугольный.
В ∆ЕОС по теореме Пифагора:
ЕС²=СО²+ЕО²
10²=8²+ЕО²
ЕО²=100–64
ЕО=√36
ЕО=6 см
Так как угол SEO=90° по условию, то ∆SEO – прямоугольный.
В ∆SEO по теореме Пифагора:
SO²=SE²+EO²
SO²=2²+6²
SO²=4+36
SO=√40
SO=2√10 см.
ответ: 2√10 см.