1. Математика
  2. Разность третьего и первого членов

Разность третьего и первого членов арифметической прогрессии равна 6, а их произведение равно 27. найти первый член и разность этой прогрессии

doschanov doschanov    1   15.08.2019 07:00    0

Ответы
almas05 almas05  25.08.2020 23:56

Арифметическая прогрессия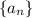  \{a_n\} с разностью  d.

a_n=a_1+d(n-1)

\displaystyle \left \{ {{a_3-a_1=6} \atop {a_3\cdot a_1=27}} \right.~~\Rightarrow~~\left \{ {{a_1+2d-a_1=6} \atop {(a_1+2d)\cdot a_1=27}} \right. \\\\\\\left \{ {{2d=6} \atop {a_1^2+2d\cdot a_1=27}} \right. ~~\Rightarrow~~\left \{ {{d=3} \atop {a_1^2+6a_1-27=0}} \right.\\\\\\a_1^2+6a_1-27=0;~~~(a_1+9)(a_1-3)=0

1) a₁ = -9;    d = 3.    Прогрессия :   -9; -6; -3; 0; 3...

2) a₁ = 3;    d = 3.    Прогрессия :     3; 6; 9; 12; 15...

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
olka52 olka52  09.05.2020 08:11
Периметр прямоугольника равен 6 дм 4 см Длина одной стороны равна 2 дм 5 см Найди длину второй стороны...
bilinia16 bilinia16  09.05.2020 08:10
Пять восьмых часть участников конкурса молодых изобретателей составляют дети до 15 лет Если общее количество участников составляет 336 человек, определите количество детей в возрасте...
фаргана4 фаргана4  09.05.2020 08:09
пазязяобъясните: переход энергии и веществ в экологической перамиде пазязя пазязя пазязя пазязя пазязя пазязя пазязя пазязя пазязя пазязя пазязя пазязя пазязя пазязя пазязя пазязя...
Мія111 Мія111  09.05.2020 08:09
Установи последовательность и продолжи ряд чисел 8, 78, 678, , ,...
Alexa647 Alexa647  09.05.2020 07:49
Самостоятельная работа по задачам на встречное движение. Работу отправляете на проверку до 9.05.Построй к задачам таблицу или чертеж. Реши задачи.№ 1.Два автомобиля одновременно...
nikusy2005 nikusy2005  09.05.2020 07:52
Теңдеулер жүйесін қосу тәсілімен шешеңдер...
дэньчик4 дэньчик4  09.05.2020 07:49
Переметр треугольника равен 42 см. Одна сторона равна 3/7 переметра, вторая сторона равна 1/3 первой стороны. Найди стороны треугольника. После похода за грибами выяснилось, что...
val40 val40  09.05.2020 07:48
от числа 74 число,если 2% его равны 29,4 ​...
AlinaVoronova AlinaVoronova  09.05.2020 07:48
А(-7:6)В(-3:2) шеңбер теңдеуін жазыңыз​...
narik2222 narik2222  09.05.2020 07:49
Как найти периметр прямоугольника,квадрата,треугольника...

Популярные вопросы