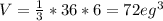Равносторонний треугольник со стороной 4√3 вращается вокруг своей высоты. Найти объём полученной фигуры вращения (Число

Question

Математика: Равносторонний треугольник со стороной 4√3 вращается вокруг своей высоты. Найти объём полученной фигуры вращения (Число π считать равным 3)

FUpp · Answer

Объём полученной фигуры вращения (тоесть конуса) = 72 ед³.

Пошаговое объяснение:

При вращении равностороннего треугольника вокруг своей высоты - получится КОНУС.

Объём конуса:

$V=\frac{1}{3}*S*h$

Где S - площадь его основания, h - высота конуса, равная высоте равностороннего треугольника.

Т.к. площадь основания - это круг, с радиусом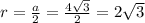 $r = \frac{a}{2}= \frac{4\sqrt{3}}{2} = 2\sqrt{3}$ ,

где a - сторона равностороннего треугольника.

Формула площади круга: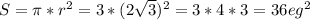 $S = \pi *r^{2} = 3*(2\sqrt{3})^{2} = 3*4*3=36 eg^{2}$

Высота равностороннего треугольника h вычисляется по формуле: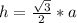 $h=\frac{\sqrt{3}}{2}*a$ ; где a - сторона равностороннего треугольника.

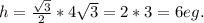
⇒ $h=\frac{\sqrt{3}}{2}*4\sqrt{3} = 2*3=6 eg.$

Подставляем полученные значения в формулу объёма конуса, и получаем: $V = \frac{1}{3}*36*6=72eg^{3}$

Равносторонний треугольник со стороной 4√3 вращается вокруг своей высоты. Найти объём полученной фиг

Равносторонний треугольник со стороной 4√3 вращается вокруг своей высоты. Найти объём полученной фигуры вращения (Число π считать равным 3)

Популярные вопросы