Равносильны ли уравнения 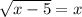 и
и 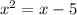 и
и 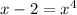
![\sqrt[4]{x-2} =/x/](/tpl/images/4165/0468/d250c.png)
Другие вопросы по теме Математика
Популярные вопросы
- Умаши и миши 18 конфет. когда маша дала мише 8 конфет, у них стало конфет...
2 - Укажите морфологические признаки слова тело...
3 - Разложить на простые множители числа...
2 - Указать морфологические признаки словам на ели , наблюдала, за ними, с тревогой,...
2 - Найдите двузначное число, если цифра единиц на 2 больше цифры десятков, а...
3 - Вставь в текст пропущенные слова. слово, стоящее в конце предыдущего предложения,...
2 - Встроке ответа запиши название материка, на котором расположена наша страна-россия....
3 - Когда были проведены реформы солона? перечислите реформы....
2 - Сравните площадь круга радиус 6см и площадь прямоугольника со соронами 6.5...
2 - Вкаком варианте ответа правильно указаны все цифры, на месте которых пишется...
3
Задание 1: образовать краткую форму прилагательных. Изменить по родам и числам
Светлый, могучий, вкусный
Чтобы выяснить, равносильно ли это уравнение уравнению
Давайте начнем с сокращения корня на первом уравнении. Возводим обе части уравнения в квадрат, чтобы избавиться от корня:
Теперь мы можем раскрыть квадрат на левой стороне уравнения:
После этого мы можем перенести все члены уравнения на одну сторону:
Таким образом, мы получаем квадратное уравнение
Теперь рассмотрим второе уравнение, представленное как
Мы можем привести его к общему виду, чтобы сравнить его с квадратным уравнением выше:
После таких преобразований мы получили четвертую степень уравнения
Теперь сравним уравнения, полученные в обоих случаях:
Первое уравнение:
Второе уравнение:
Мы можем видеть, что квадратное уравнение имеет степень 2 (потому что старшая степень в уравнении - это 2) и уравнение четвертой степени имеет степень 4 (потому что старшая степень в уравнении - это 4).
Таким образом, уравнения не равносильны, потому что они имеют разные степени.
Вывод: Уравнения
Теперь давайте перейдем ко вторым уравнениям:
Аналогично первому случаю, давайте приведем их к общему виду:
Мы видим, что и первое уравнение, и второе уравнение имеют одинаковую степень 4.
Теперь сравним уравнения:
Первое уравнение:
Второе уравнение:
Мы можем видеть, что оба уравнения имеют степень 4, значит они равносильны.
Вывод: Уравнения