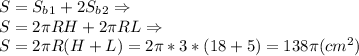Равнобедренная трапеция с основаниями 10 см и 18 см и высотой 3 см вращается около меньшего основания. найдите площадь поверхности тела вращения

Смотри в приложении:

138π см²

Пошаговое объяснение:

Построим равнобедренную трапецию ABCD с высотой CF (см. Рис. 1).

Согласно условию: AD=18 см,  BC=10 см,  CF=3 см. Для дальнейших вычислений нам понадобится длина боковой стороны трапеции AB=CD.

Т.к. трапеция равнобедренная, то FD = (AD-BC):2 = 4 см.

ΔCDF - прямоугольный с катетами CF=3 см, FD=4 см, значит он египетский, и его гипотенуза CD=5 см.

При вращении такой трапеции вокруг короткого основания образуется цилиндр с равными осевыми конусообразными выемками с обеих сторон (См. рис. 1.2, 2.1, 2.2). Радиус такого цилиндра равен высоте трапеции R=CF=3 см, а высота цилиндра равна длинному основанию трапеции H=AD=18 см.

Образующей конуса-выемки является боковая сторона трапеции L=CD=5 см, радиус равен радиусу цилиндра R=3 см.

Искомая площадь полной поверхности  фигуры вращения состоит из площади боковой поверхности цилиндра и двух боковых поверхностей конусов-выемок.

Площадь боковой поверхности цилиндра: .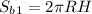

Площадь боковой поверхности конуса-выемки: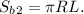

Площадь полной поверхности: