Расстояние между а и b равно 600 км. из города а в город в выехал автомобиль, а через 2 часа следом за ним со скоростью 90 км/ч выехал мотоциклист, догнал автомобиль в городе с и повернул обратно. когда он вернулся в а, автомобиль прибыл в в. найдите скорость автомобиля. с подробным решением, : )

Ответы

sdk2 07.10.2020 16:14

Пусть x км/ч - скорость автомобиля. Мотоциклист проехал 2х км, то автомобилю оставалось проехать (600-2х) км. Скорость сближения - (90-х) км/ч. Когда мотоциклист обогнал автомобиля, то обратно в пункт А проехал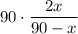 $90\cdot \dfrac{2x}{90-x}$ км, а автомобилю осталось проехать 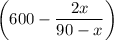$\bigg(600-\dfrac{2x}{90-x} \bigg)$ км в пункт В.

Из условия время прибытия мотоциклиста в пункт А и автомобиля в пункт В равны, то есть: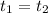 t_1=t_2

$\dfrac{2x}{90-x} =\dfrac{600-\dfrac{2x}{90-x} }{x} \\ \\ \\ x^2=300(90-x)-90x\\ \\ x^2+390x-390\cdot90=0\\ \\ D=39^2\cdot10^2+4\cdot 300\cdot90=10^2\cdot9\cdot(13^2+120)=10^2\cdot9\cdot17^2\\ \\ \sqrt{D} = \sqrt{10^2\cdot9\cdot17^2}=10\cdot3\cdot17=510$

x_1=-450 - не удовлетворяет условию

x_2=60 км/ч - скорость автомобиля

ОТВЕТ: 60 км/ч.

ПОКАЗАТЬ ОТВЕТЫ

312645 07.10.2020 16:14

Дано:

S=600 км

Vм. = 90 км/ч

tз. = 2 ч

Найти:

Vа. км/ч

x ч - время мотоциклиста до города С

(2+х) ч - время автомобиля до города С

(2+2х) ч - время автомобиля от города А до B

Va.=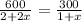 $\frac{600}{2+2x} = \frac{300}{1+x}$

Найдем x:

$\frac{300}{1+x} * (2+x)=90x \\ \\ 600(2+x)=90x(2+2x) \\ \\ 1200+600x=180x+180x^{2} \\ \\ -180x^{2}+420x+1200=0\ | : (-60)\\ \\ 3x^{2}-7x-20=0 \\ \\ D=b^{2}-4ac=49+240=289, x0 \\ \\ x_{1}=\frac{7-17}{6}= -\frac{5}{3} - ne ydovletvor`aet yslovie$

$x_{2}=\frac{7+17}{6}= 4$

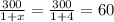Va.= $\frac{300}{1+x} = \frac{300}{1+4} = 60$ (км/ч)

ответ: 60 км/ч

ПОКАЗАТЬ ОТВЕТЫ

kayot1 12.01.2024 10:41

Добрый день!

Для решения данной задачи нам необходимо использовать формулу расстояния, времени и скорости: расстояние = скорость x время.

Обозначим скорость автомобиля как V_автомобиль, а время, за которое автомобиль доехал до города В, как t_автомобиль.

Также обозначим скорость мотоциклиста как V_мотоциклист и время его поездки как t_мотоциклист.

Из условия задачи известно, что расстояние между городами а и В равно 600 км, поэтому:
600 км = V_автомобиль x t_автомобиль -------> (1).

Согласно условию задачи, мотоциклист выехал из города а через 2 часа после автомобиля, поэтому t_мотоциклист = t_автомобиль - 2.

Мотоциклист догнал автомобиль в городе с и повернул обратно. Это значит, что мотоциклист проехал расстояние, равное расстоянию между городами а и с. После этого он вернулся обратно в город а. Таким образом, мотоциклист проехал двойное расстояние между городами а и с.

Используя формулу расстояния, времени и скорости, можем составить уравнение:
2 x 600 км = V_мотоциклист x t_мотоциклист -------> (2).

Теперь у нас есть два уравнения с двумя неизвестными (V_автомобиль и t_автомобиль), и мы можем решить систему этих уравнений.

Из уравнения (1) выразим t_автомобиль:
t_автомобиль = 600 км / V_автомобиль.

Подставим это значение в уравнение (2):
2 x 600 км = V_мотоциклист x (600 км / V_автомобиль - 2).

Распишем уравнение подробнее:

1200 км = 600 км x (600 км / V_автомобиль - 2).

Домножим обе части уравнения на V_автомобиль:

1200 км x V_автомобиль = 600 км x (600 км - 2V_автомобиль).

Раскроем скобки:

1200 км x V_автомобиль = 360000 км^2 - 1200 км x V_автомобиль.

Перенесем все, относящееся к V_автомобиль, в одну часть уравнения:

2 x 1200 км x V_автомобиль = 360000 км^2.

Упростим выражение:

2400 км x V_автомобиль = 360000 км^2.

Разделим обе части уравнения на 2400 км:

V_автомобиль = 360000 км^2 / 2400 км.

Вычислим это значение:

V_автомобиль = 150 км/ч.

Таким образом, скорость автомобиля равна 150 км/ч.

Надеюсь, что это подробное и обстоятельное решение поможет вам понять, как нужно решать подобные задачи. Если у вас возникнут еще вопросы, не стесняйтесь задавать их!

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Математика