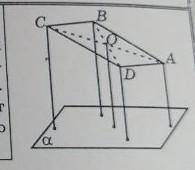
расстаяние от точки О пересечения диагоналей параллелограмма Abcd, не пересекающего плоскость альфа, до этой плоскости 5 см. Найдите сумму расстояний от всех вершин параллелограмма до плоскости альфа
Другие вопросы по теме Математика
Популярные вопросы
- Якщо вид задуманого числа знайти 80%, а потим вид отриманого числа знайти ще 80%...
1 - Зміна природних и ранамим із зміннино температури повітря кількості опадів у вертикалыпкиму...
2 - Установить соответствии подскажите...
3 - решить, осталось 30 минут решить, осталось 30 минут >...
1 - сложения подстановки сложения подстановки >...
2 - 1)Почему являясь универсальным товаром денги воспринимаються как ценности ? 2)...
2 - Решите уравнение:3,5x-4,9равно1,4x+1,4...
1 - В каком году произошло крежение руси...
3 - Определите событие, о котором идет речь. «Грушараздора». 3 богини: Афина, Артемида...
3 - Составить уравнения реакций, при которых можно осуществить следующие превращения:...
3
Чтобы ответить на ваш вопрос, давайте разберемся пошагово.
1. Параллелограмм Abcd имеет точку пересечения диагоналей О.
2. Мы знаем, что расстояние от точки О до плоскости альфа составляет 5 см.
3. Нам нужно найти сумму расстояний от каждой из вершин параллелограмма до плоскости альфа.
Чтобы решить эту задачу, мы можем использовать свойства параллелограмма и плоскости.
1. Сначала найдем высоту параллелограмма, то есть расстояние от одной из его сторон до противоположной.
Найдем высоту из треугольника ОАС, где А и С - это вершины параллелограмма, а О - точка пересечения диагоналей.
Для этого воспользуемся формулой для вычисления площади треугольника: S = 0.5 * a * h, где а - основание, а h - высота.
Пусть а = АС, а h - высота из ОАС.
2. Теперь найдем площадь параллелограмма, используя один из методов.
Мы можем использовать формулу площади через длину основания и высоту, S = a * h.
В нашем случае основание а равно АС, а высота - высота параллелограмма, найденная в предыдущем шаге.
Обозначим площадь параллелограмма через S_пар.
3. Следующим шагом найдем площадь треугольника ОAS.
Так как параллелограмм Abcd - это два равнобедренных треугольника по основанию АС, площадь одного из треугольников можно найти по формуле S_тр = 0.5 * АС * h.
Для нахождения площади треугольника ОАС, умножим S_тр на 2.
4. Далее найдем площадь треугольника ОА(параллелограмма Abs).
Он также является равнобедренным треугольником по основанию ОА.
Используя формулу площади треугольника (S_тр = 0.5 * ОА * h), найдем площадь треугольника ОА, где основание - это ОА.
5. Наконец, чтобы найти сумму расстояний от всех вершин параллелограмма до плоскости альфа, сложим длину отрезка из каждой вершины параллелограмма до плоскости.
Таким образом, шаг за шагом мы можем решить эту задачу, используя свойства параллелограмма и плоскости, а также формулы для вычисления площадей треугольников и параллелограммов.
Надеюсь, это поможет вам понять и решить данную задачу. Если у вас возникнут еще вопросы, обращайтесь!