Распишите решение через дискриминант −4x^2+52x−144=0
Узнать дискриминант и решение x1 и x2
Другие вопросы по теме Математика
Популярные вопросы
- А)столик трава поля моря б)мороз страна молоко ученик в)море слезы вода...
1 - Билет № 4 1. расскажите, как образуется повелительное наклонение в языке....
1 - 1. в каком ряду все прилагательные образованы приставочным подгорный,...
3 - Престройте так, чтобы деепричастный оборот находился в начале, середине...
3 - Впоезде едут пассажиры иванов, петров и сидоров. оказалось, что такие...
2 - Прочитайте повесть гоголя ночь перед рождеством 1.кто главный герой повести(внешность,душевные...
2 - Найди периметр и плошадь земельных участков по указанным размерам.что...
2 - Почему укрепление на юге руси иногда называют змиевыми валами ?...
2 - Сочинение муму самый трогательный эпизод...
3 - Составьте уравнение для решения : «в x корзин насыпали по 13 кг груш,...
2
Відповідь: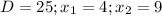
Покрокове пояснення:
4; 9
Пошаговое объяснение:
Задание: решить уравнение –4х²+52х–144=0.
Решение:Разделим обе части уравнения на "-4", чтобы квадратное уравнение стало приведённым.
х² - 13х + 36 = 0. Запишем коэффициенты:
а=1; b=-13; c=36.
Формула дискриминанта: D=b²–4ac.Подставим наши данные:
D = (-13)² - 4 · 1 · 36 = 169 - 144 = 25.
Дискриминант уравнения равен 25.
Запишем формулы корней:Подставим наши данные: