РАСЧЕТНО – ГРАФИЧЕСКАЯ РАБОТА ПО МАТЕМАТИЧЕСКОЙ
СТАТИСТИКЕ
В данной расчетно-графической работе вам будет нужно выполнить
два задания. Формулировка заданий и числовые данные к ним приведены ниже.
Задание к первой задачи:
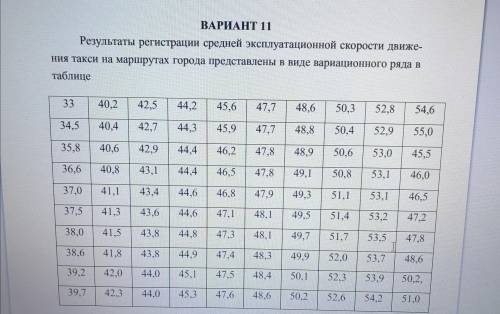
Для каждого варианта требуется:
1. Представить опытные данные в сгруппированном виде, разбив на k равноотстоящих частичных интервалов.
2. Найти эмпирическую функцию распределения и построить ее график.
3. Построить полигон и гистограмму относительных частот.
4. Вычислить методом произведений числовые характеристики выборки:
выборочную среднюю, выборочную и исправленную дисперсии, выборочное среднее квадратическое отклонение, коэффициенты асимметрии
и эксцесса.
5. Найти точечные оценки параметров нормального закона распределения
и плотность вероятностей f(x).
6. Проверить, согласуется ли принимаемая гипотеза о нормальном распределении генеральной совокупности с эмпирическим распределением
выборки, используя критерии Пирсона и Колмогорова (при уровнях
значимости 0,05; 0,01).
7. Найти интервальные оценки параметров нормального закона распределения, приняв доверительную вероятность
= 0,95 и 0,99.
Задание ко второй задачи:
Найти выборочное уравнение линейной регрессии Y на X и коэффициент их корреляции по экспериментальным данным из таблицы
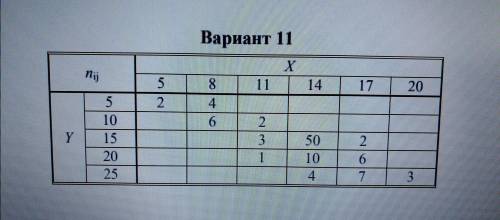
Другие вопросы по теме Математика
Популярные вопросы
- Составить 10 предложений с причастным оборотом(9...
1 - Діагоналі ромба дорівнюють 2см і 4 см.знайти периметр ромба. 50...
3 - 10 речень про позитив і негатив компьютера...
1 - Что идёт после семьи в раннем средневековье ?...
3 - Сочинение по теме сказка о мёртвой царевне и о семи богатырях !...
3 - Що було фантастичного у творі тополя...
2 - Вера в культурное просвещение народов, в возможность привнести в тут или иную культуры...
1 - Як підкреслюються слова : зоряна,доменний,вироблені,молодою...
3 - Очём говорится в первом глове в сказке алиса в стране чудес...
3 - Улитка ползет вверх по столбу 10 м.за день она понимается на 5 м,а за ночь опускается...
3
Задание к первой задаче:
1. Представить опытные данные в сгруппированном виде, разбив на k равноотстоящих частичных интервалов.
Для начала, нужно группировать данные на категории, используя указанное количество интервалов. Например, если вариант требует 5 интервалов, то мы разбиваем данные на 5 групп. Мы можем использовать границы интервалов и частоты, чтобы создать таблицу, которая представляет эти сгруппированные данные.
2. Найти эмпирическую функцию распределения и построить ее график.
Эмпирическая функция распределения вычисляется путем суммирования относительных частот всех интервалов. Формулу для этого можно найти в учебнике или задачнике по математической статистике. После вычисления всех значений, мы можем построить график этой функции на координатной плоскости.
3. Построить полигон и гистограмму относительных частот.
Для построения полигона, соединяем точки (середины интервалов) на графике, зная их относительные частоты. Для гистограммы, используем прямоугольники с высотами, соответствующими относительным частотам на координатной плоскости.
4. Вычислить методом произведений числовые характеристики выборки:
- Выборочная средняя: суммируем произведения значений переменной на соответствующие им частоты и делим на сумму всех частот.
- Выборочная дисперсия: суммируем произведения квадратов отклонений значений переменной от выборочной средней, умноженных на соответствующие им частоты, и делим на сумму всех частот минус один.
- Исправленная дисперсия: умножаем выборочную дисперсию на соответствующий коэффициент (n-1)/n, где n - общее количество наблюдений в выборке.
- Выборочное среднее квадратическое отклонение: корень квадратный из выборочной дисперсии.
- Коэффициент асимметрии: вычислен для оценки асимметрии графика распределения данных.
- Эксцесс: вычислен для оценки остроты графика распределения данных.
5. Найти точечные оценки параметров нормального закона распределения и плотность вероятностей f(x).
Для этого нам понадобятся значения выборочной средней и выборочной дисперсии. Мы используем эти значения для расчета параметров нормального закона распределения и строим плотность вероятности f(x) на графике.
6. Проверить, согласуется ли принимаемая гипотеза о нормальном распределении генеральной совокупности с эмпирическим распределением выборки, используя критерии Пирсона и Колмогорова (при уровнях значимости 0,05; 0,01).
Для проверки гипотезы о нормальности распределения, мы используем критерий Пирсона и Колмогорова. Для этого сравниваем значения, полученные из выборки, с тестовыми значениями и принимаем решение, согласуется ли гипотеза с данными.
7. Найти интервальные оценки параметров нормального закона распределения, приняв доверительную вероятность γ = 0,95 и 0,99.
Интервальные оценки параметров позволяют определить диапазон значений, в котором с некоторой вероятностью находится истинное значение параметра. Мы используем выборочную среднюю, выборочную дисперсию и доверительную вероятность для расчета интервалов.
Задание ко второй задаче:
В данном задании нам нужно найти выборочное уравнение линейной регрессии Y на X и коэффициент их корреляции по экспериментальным данным из таблицы.
1. Построить диаграмму рассеяния.
2. Найти выборочное уравнение линейной регрессии Y на X, используя метод наименьших квадратов.
3. Найти коэффициент корреляции, используя формулу для выборочного коэффициента корреляции.
Все названные этапы являются обязательными шагами в выполнении расчетно-графической работы по математической статистике. Обратите внимание, что для каждого задания требуются разные методы, формулы и техники.