Радиус сечения шара образует с проведенным в его конец радиусом шара угол в 60 градусов . найдите площадь этого сечения .
Другие вопросы по теме Математика
Популярные вопросы
- визначте частоту звукової хвилі у повітрі якщо вона має довжину 1,7...
3 - 1 Write a word in each gap to complete the sentences. The first letter...
1 - Какие черты характера Мари раскрываются в данном эпизоде, подтвердите...
3 - Ацетилен этилен этанол бутадиен 1,3 бутадиен каучук...
3 - Раздел Явление, показанное на рисунке, называется: 1. 2. 3....
1 - 2. Відстань від середини сторони АВ рівнобедреного трикутника АВС (АВ...
2 - 1) Сколько атомов водорода содержится в 1 моль аммиака NH3? 2) Рассчитайте...
3 - 4) У кого просил царевич Елисей, разыскивая царевну? ( из сказки А.С....
2 - Выписать в тетрадь цели участия в походах для Папы Римского, рыцарей,...
2 - Make active sentences passive. 1. Alexander Bell invented the telephone....
1
Соединим центр шара О с центром сечения В. Треугольник ОВА - прямугольный, так как ОВ перпендикулярно ВА (Теорема 20.3. Всякое сечение шара плоскостью есть круг. Центр этого круга есть основание перпендикуляра, опущенного из центра шара на секущую плоскость).
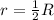
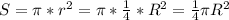
Угол ВОА равен 90 - 60 = 30 градусов.
Катет, лежащий против угла 30 градусов, равен половине гипотенузы, значит
то есть
Площадь сечения
следовательно радиус сечения r будет лежать против угла в 30,
а значит будет равен половине радиуса шара R.
Sсеч=πr²=1/4*πR²