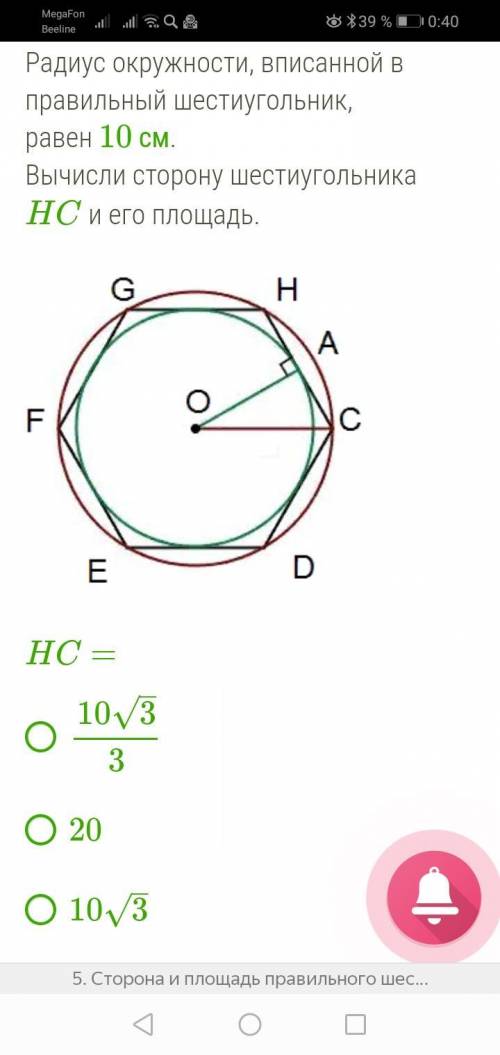
Радиус окружности, вписанной в правильный шестиугольник, равен 10 см.
Вычисли сторону шестиугольника HC и его площадь.

6sturisA_F.png

HC=
103–√3
20
103–√
203–√3
203–√
10
см .

S=
203–√
100
1003–√
2003–√
20
200
см2 .

Хорошо, давай разберемся с этой задачей.

Дано, что радиус окружности, вписанной в правильный шестиугольник, равен 10 см. Для начала, нам понадобится понять, как радиус вписанной окружности связан с стороной шестиугольника.

Если мы нарисуем радиус окружности (зеленый луч), вписанной в шестиугольник, то сторона шестиугольника будет разделена на две равные части. Каждая из этих частей будет являться радиусом окружности (синий отрезок).



Также, если мы нарисуем высоту шестиугольника (красный отрезок) из центра окружности, она будет являться радиусом вписанной окружности.

Поскольку шестиугольник является правильным, у него все стороны и углы равны. Значит, высота шестиугольника будет являться высотой равнобедренного треугольника (углы основания треугольника тоже равны, потому что треугольник равнобедренный).

Теперь можем перейти к решению. Мы знаем, что радиус окружности равен 10 см. Мы хотим найти сторону шестиугольника HC и его площадь.

1. Разделим сторону шестиугольника на две равные части, чтобы найти радиус окружности.

Для этого воспользуемся формулой длины окружности. Длина окружности вычисляется по формуле: L = 2πr, где L - длина окружности, r - радиус окружности.

В нашем случае, длина окружности будет равна периметру шестиугольника, поскольку она проходит через все вершины шестиугольника. Также, поскольку шестиугольник равносторонний, его периметр будет равен 6 * HC (так как шестиугольник имеет шесть сторон).

Значит, у нас есть уравнение: 2π * r = 6 * HC.

2. Найдем радиус окружности.

Так как мы знаем, что радиус окружности равен 10 см, можем подставить его в уравнение:

2π * 10 = 6 * HC.

Упрощая уравнение, получаем: HC = (2π * 10) / 6.

3. Вычислим значение HC.

Подставим числовые значения в формулу:

HC = (2π * 10) / 6 = (20π / 3) ≈ 10.47 см.

Таким образом, сторона шестиугольника HC равна примерно 10.47 см.

Теперь перейдем к вычислению площади шестиугольника.

4. Найдем площадь шестиугольника.

Площадь правильного шестиугольника можно найти, зная его сторону HC. Формула для вычисления площади правильного шестиугольника: S = (3 * √3 * a^2) / 2, где S - площадь, a - сторона шестиугольника.

Подставим значение HC в формулу:

S = (3 * √3 * 10.47^2) / 2.

5. Вычислим значение S.

Выполним вычисления:

S = (3 * √3 * 10.47^2) / 2 ≈ 270.61 см^2.

Таким образом, площадь шестиугольника составляет примерно 270.61 см^2.

Итак, ответ на задачу:
- Сторона шестиугольника HC равна примерно 10.47 см.
- Площадь шестиугольника составляет примерно 270.61 см^2.