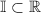Рационал (Q), иррационал (I) және нақты (R) сандар үшін дұрыс қатынасты анықтау керек A) Q∪R=I B) I ⊂ R C) I ⊂Q D) R⊂Q E) Q ⊂ I Перевела онлайн переводчиком Для рациональных (Q), иррациональных (I) и точных (R) чисел необходимо определить правильное отношение A) Q∪R=I B) I ⊂ R C) I ⊂Q D) R⊂Q E) Q ⊂ I
Другие вопросы по теме Математика
Популярные вопросы
- Стр. 110 выучить таблицу , правило упр. 231 ( устно) Упр. 232 (...
1 - по братскии , это очень Задание по экологии, нужно охарактеризовать...
3 - Написать сочинение на тему Все мы жили рядом с ней и не поняли,...
1 - Під якими назвами згадуються слов яни в історичних документах? (3...
1 - Ви побачили що підкілти влаштовують бійку запишіть ваші дії...
1 - Помагите Fill in prepositions with, in, by, on where it is necessary...
1 - Захар Прилепин. Рассказ Белый квадрат Прочитать рассказ и дать характеристику...
3 - Северный полярный круг – это граница области, куда в любое время...
2 - Предвидите пример использования кислоты или основания в домашнем...
2 - Пан Журден хотів стати а)лицарем б)шляхтичем в)буржуа г)актором...
2
Множество действительных чисел есть объединение двух непересекающихся множеств: множества рациональных чисел и множества иррациональных чисел:
Из этого соотношения можно сделать два основных вывода:
Из вариантов ответов правильным является В)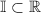
Остальные ответы неверны вот почему:
А) , так как при объединении множеств
, так как при объединении множеств  и
и 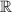 получается множество
получается множество 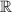
С)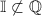 , так как никакое иррациональное число не является рациональным
, так как никакое иррациональное число не является рациональным
D)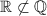 , так как не всякое действительное число является рациональным
, так как не всякое действительное число является рациональным
Е)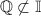 , так как никакое рациональное число не является иррациональным
, так как никакое рациональное число не является иррациональным
Правильный соотношение В)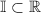
ответ: В)