Пусть неправильная дробь p/q несократима. Может ли оказаться сократимой правильная дробь - дробная часть полученной из неё смешанной дроби? Как доказать .

Пошаговое объяснение:

Алгоритм Евклида.

Пусть a = b⋅q + r, тогда НОД (a, b) = НОД (b, r)

Из чего вытекает несократимость дробной части

Предположим, дробная часть a/b- сокращается в отличии от неправильной дроби (bc+a)/b где целая часть это число с

a/b- сокращается⇒НОД(a; b)=k>1, числа a и b делятся на число k

a=nk, b=mk⇒bc+a=cmk+nk=k(cm+n)⇒НОД(bc+a; b)≥k>1

То есть неправильная дробь тоже сократима.

Пришли к противоречию. Значит, наше предположение было неверным.

Нет

Пошаговое объяснение:

Так как дробь неправильная, то .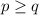

Тогда пусть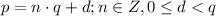 [очевидно, такое представление существует: 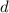- это остаток, а 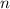- частное от деления с остатком 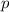на ]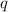

Тогда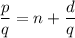

Очевидно,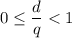 , а значит - рассматриваемая дробная часть.

Пусть d и q имеют общий простой множитель s, т.е. дробь сократима. Но тогда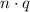 также делится на s - а значит и 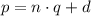делится на s, то есть исходная дробь  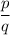 сократима - противоречие с условием.

Значит, рассматриваемая дробная часть несократима