Пусть f - многочлен, а F - множество решений уравнения f(x) = х - совпадает с множеством решений уравнения f(f(x)) = x.
Покажите, что множество решений уравнения f(f(...(x)...)) совпадает с F.
Другие вопросы по теме Математика
Популярные вопросы
- Презентация о форме государственного правления германии , . мне это надо на завтра...
3 - Чем отличается уважение от чинопочитание в рассказе толстый и тонкий...
2 - Чего в 17 веке было меньше 3 (трёх)...
2 - Выберите разницу в местном времени г. уфа (55°с.ш. 56°в.д.) и г. армавира (45°с.ш....
1 - Составьте поздравительное смс сообщение другу...
1 - Как мы познаем мир? 5 органов чувств сочинение...
3 - Сделать морфологический разбор слов зиму и постели поиз сфоткайте...
2 - Командующий волнами в семилетней войны...
3 - Авечером папа спросил : ,, ну как понравилось в цирке? нужна схема...
2 - Составить 5 предложений с наречиями и использовать в них слова: 1.поднявший 2.жалюзи...
2
Пусть означает
означает  , где
, где  применена
применена  раз.
раз.
Поскольку многочлен, то у него есть значение в любой точке. (*)
многочлен, то у него есть значение в любой точке. (*)
Докажем утверждение по индукции.
База: - это то, что дано по условию.
- это то, что дано по условию.
Переход:
Пусть для некоторого верно; Докажем, что из этого следует справедливость утверждения и для
верно; Докажем, что из этого следует справедливость утверждения и для  ; Действительно, по предположению индукции множество решений уравнения
; Действительно, по предположению индукции множество решений уравнения  совпадает с
совпадает с  ; Возьмем
; Возьмем  от обеих частей (благодаря (*) мы можем это сделать):
от обеих частей (благодаря (*) мы можем это сделать):  ; Но если сделать замену
; Но если сделать замену  , получим
, получим  ; А множество решений этого уравнения лежит в
; А множество решений этого уравнения лежит в  ; Предположим, что есть некоторый элемент
; Предположим, что есть некоторый элемент  , такой, что для него не найдется
, такой, что для него не найдется  , чтобы
, чтобы  ; Тогда
; Тогда 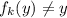 , но
, но  лежит в
лежит в  , противоречие. Это завершает переход.
, противоречие. Это завершает переход.